🐣 4. Trees and Graphs

4. Trees and Graphs

📚 1. 트리의 종류

• 재귀적 설명법
• 노드로 이루어진 자료 구조
• 하나의 루트 노드를 가짐

• 재귀 (아래 구조 반복)
  • 루트 노드 : 0개 이상의 자식 노드
  • 자식 노드 : 0개 이상의 자식 노드

• 사이클 존재 ❌
• 각 노드는 어떤 자료형으로도 표현 가능

class Node {
	public String name;
	public Node[] children;
}

💡 Node 클래스를 포함하도록 Tree 클래스를 정의할 수 있지만.. 굳이..? 사용한다고 해서 코드가 더 좋아지진 않음

class Tree {
	public Node root;
}

트리 🆚 이진 트리

• 이진 트리(binara tree)
  • 각 노드가 최대 두 개의 자식을 갖는 트리
  • 자식이 없는 노드 : 말단 노드(Nil)

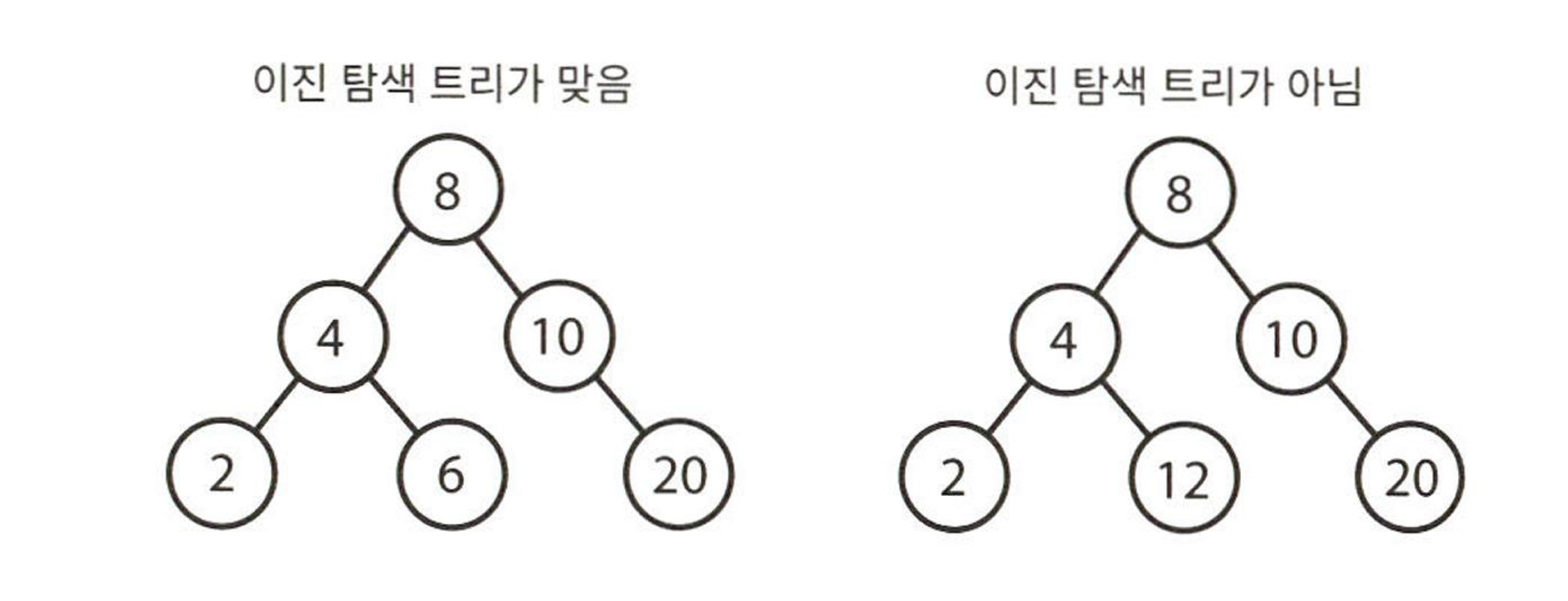
이진 트리 🆚 이진 탐색 트리

• ${모든 왼쪽 자식들} <= n < {모든 오른쪽 자식들}$ 의 속성은 모든 노드 n에 대하여 항상 참
• 부등식은 내 밑에 있는 모든 자식 노드들에 대해서 참이어야함

⭐️ 이진 탐색 트리에서 같은 값을 처리하는 방식

1. 트리는 중복된 값을 가지면 안된다?
2. 중복된 값은 오른쪽 혹은 양쪽 어느 곳이든 존재할 수 있다?

👉🏻 모두 맞는 말이므로 처음에 트리의 정의를 어떻게 하느냐에 따라 달려있다.

💡 트리 문제가 주어지면 이진 탐색 트리일 것이라고 가정하는 경우가 많음 (⇢ 인터뷰 문제로 제시되면 이진 탐색 트리인지 아닌지 확실히 물어봐야함)

균형 🆚 비균형

• ‘균형’ 트리
  • $O(logN)$ 시간에 insert 와 find 를 할 수 있을 정도로 균형이 잘 잡혀있다를 대충 척도롤 삼는다.
• e.g. ‘레드-블랙 트리’, ‘AVL 트리’

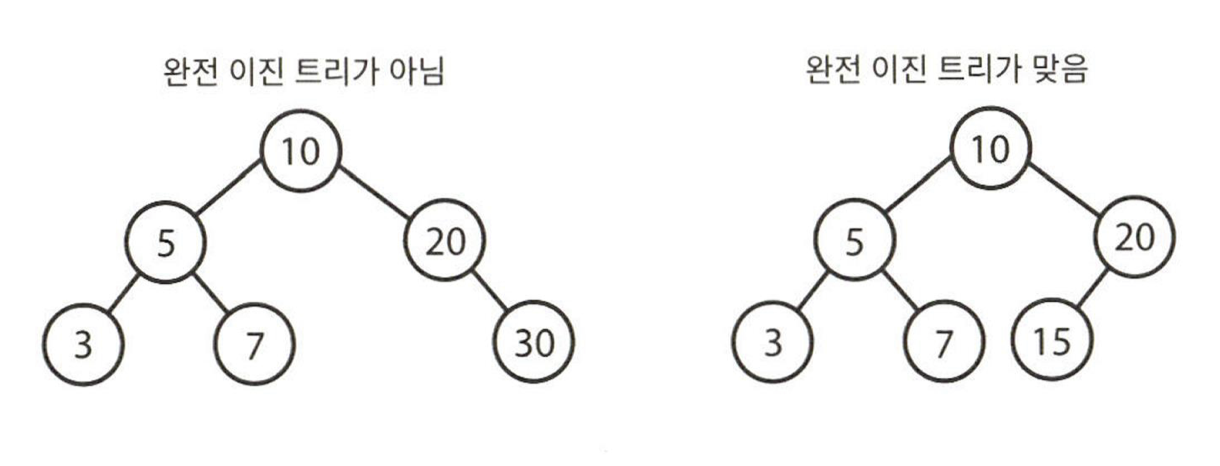
완전 이진 트리

• 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리
• 마지막 단계에는 꽉 차 있지 않아도 되지만 노드가 좌에서 우로 채워져야한다.

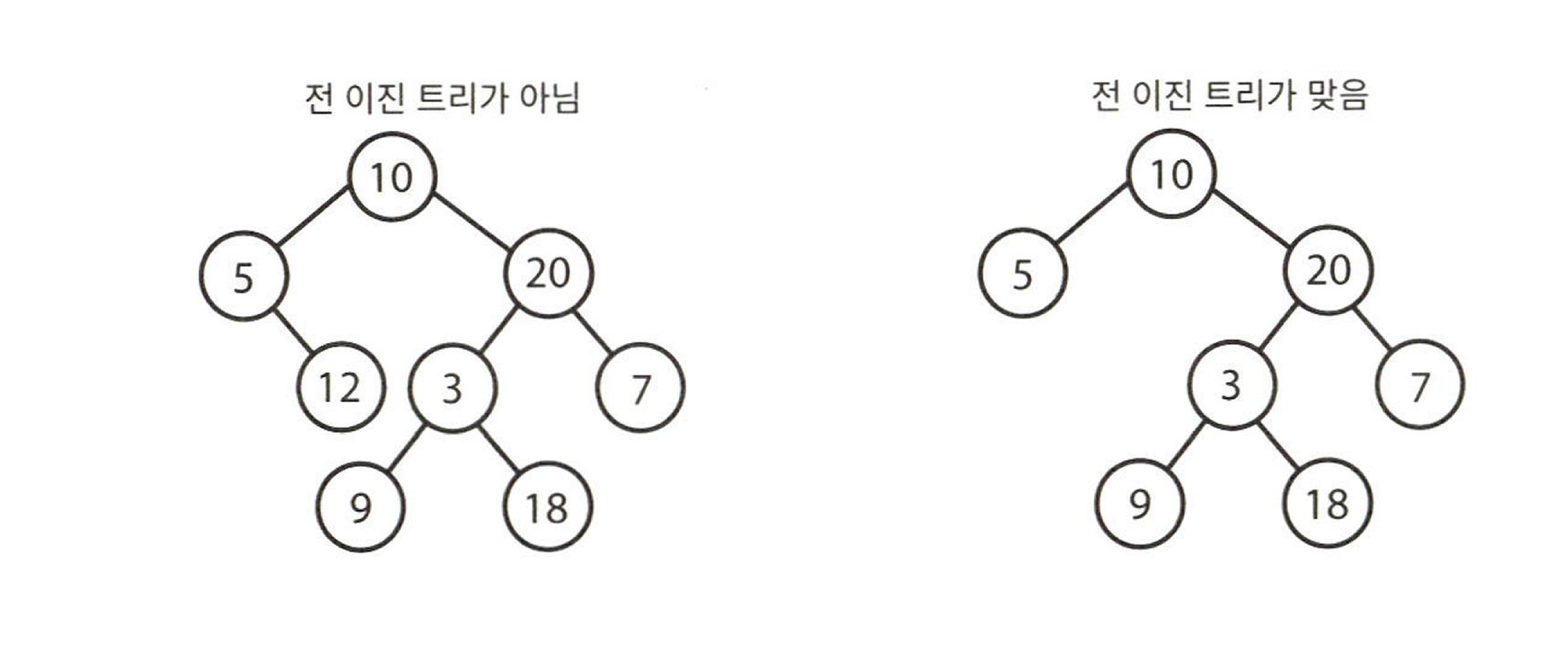
전 이진 트리

• 모든 노드의 자식이 없거나 정확히 두 개 있는 경우
• 자식 하나만 있는 노드 ❌

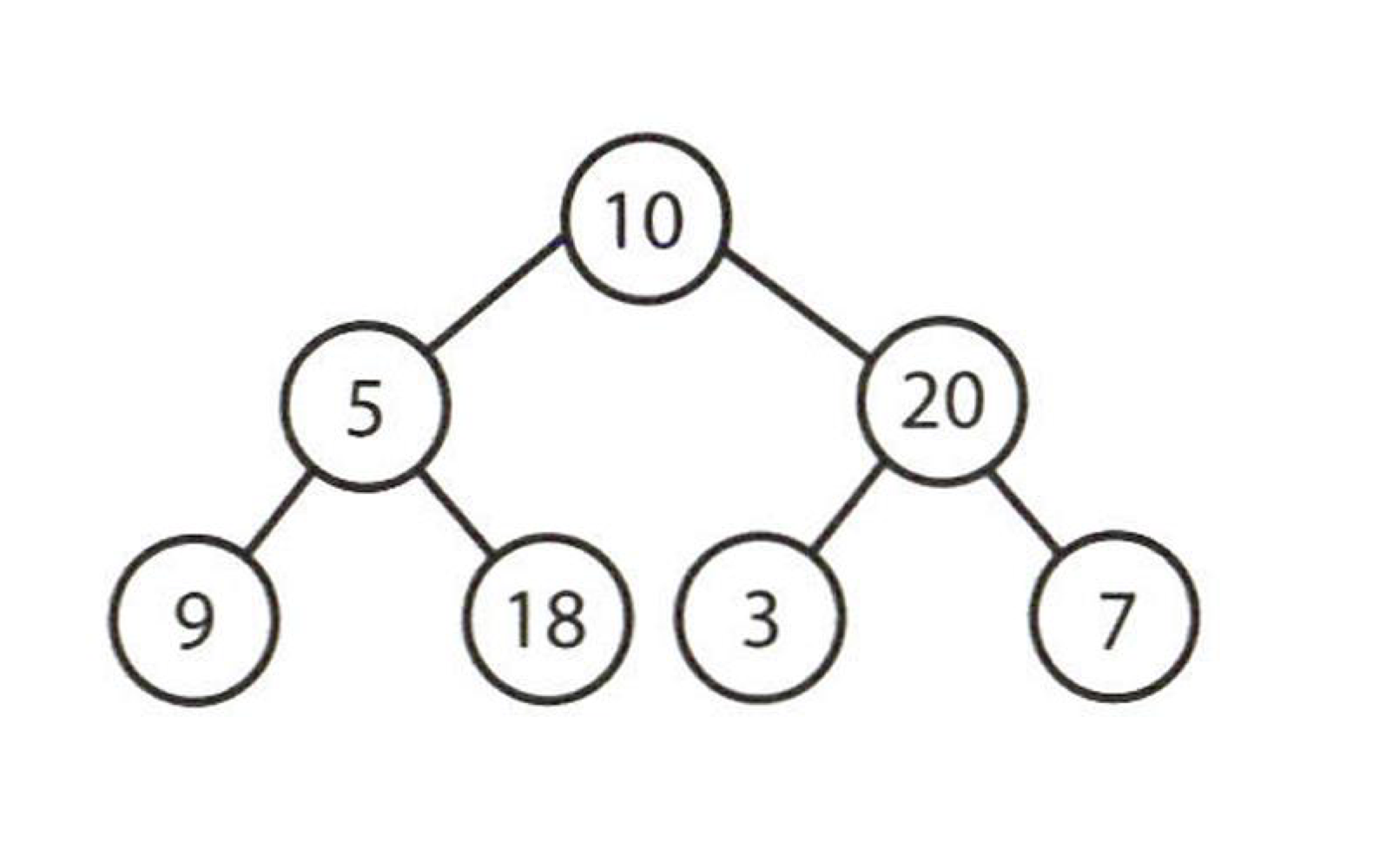
포화 이진 트리

• 전 이진 트리이면서 완전 이진 트리인 경우
• 마지막 단계에서 노드의 개수가 최대가 되어야함
• 노드의 개수가 정확히 $2^{k-1}$ 개 ($k$ : 높이)

이진 트리 순회

💡 루트 노드의 순회 순서에 따라 명명

• 중위 순회

void inOrderTraversal(TreeNode node) {
  if (node != null) {
    inOrderTraversal(node.left);
    visite(node);
    inOrderTraversal(node.right);
  }
}

• 전위 순회

void preTraverse(TreeNode node) {
  if (node != null) {
    visit(node);
    preTraverse(node.left);
    preTraverse(node.right);
  }
}

• 후위 순회

void postTraverse(TreeNode node) {
  if (node != null) {
    postTraverse(node.left);
    postTraverse(node.right);
    visit(node);
  }
}

이진 힙(최소/최대 힙)

• 최소힙(min-heaps)
  • 원소 오름차순 정렬
• 최대힙(max-heaps)
  • 원소 내림차순 정렬

• 최소힙 💡 최대힙은 최소힙과 방식이 완전히 동일(정렬 순서만 다름)
• 완전 이진 트리
• 각 노드의 원소가 자식들의 원소보다 작다
• 루트 : 트리 전체에서 가장 작은 원소

• 연산
  • insert
  • extract_min

• 삽입
• $O(log n)$ 소요

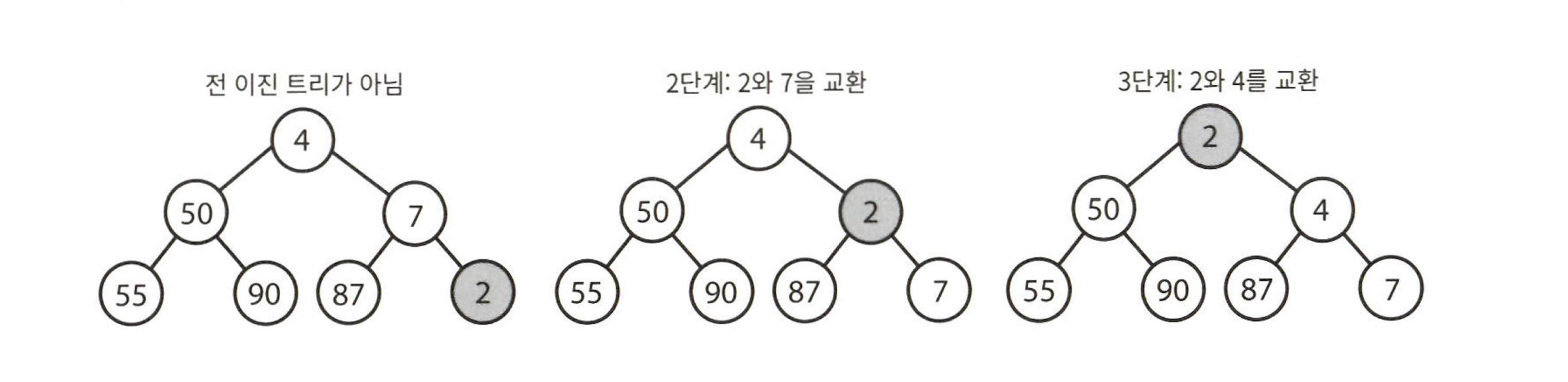
• 트리의 밑바닥에서부터 삽입
• 새로운 원소 : 밑바닥 가장 오른쪽 위치로 삽입
• 새로 삽입된 원소가 제대로 된 자리 찾을 때까지 부모 노드와 교환 -> 최소 원소를 위쪽으로 올림

• 최소 원소 뽑아내기
• $O(log n)$ 소요

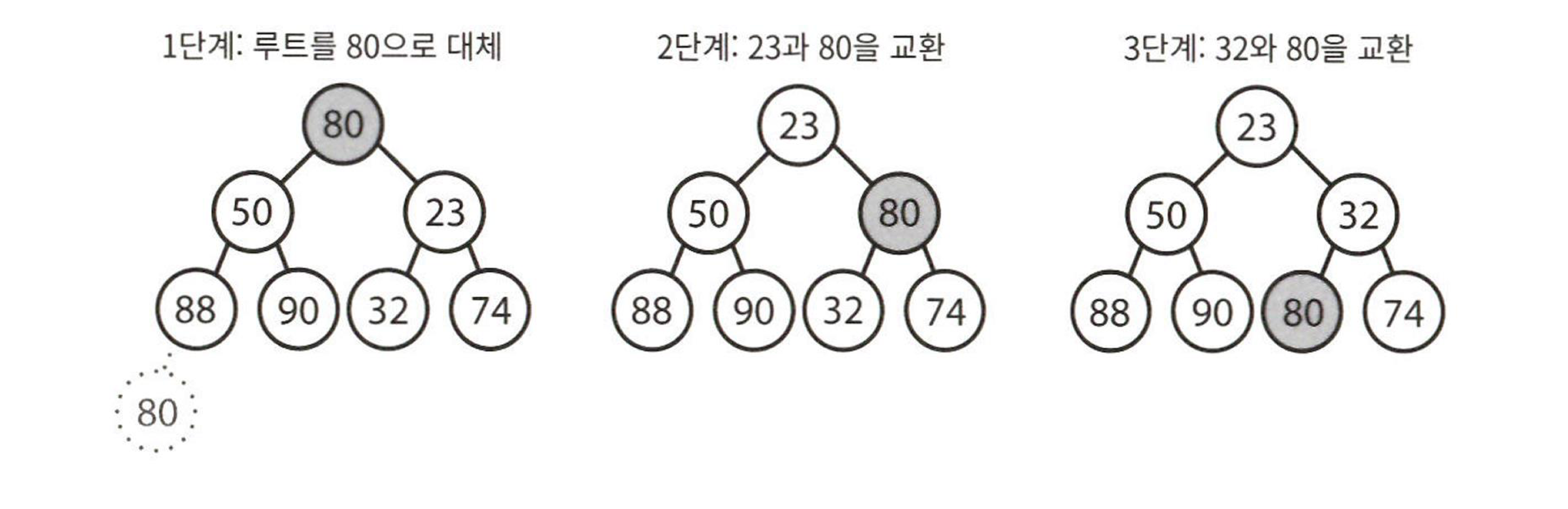
• 최소 원소를 제거한 후에 힙에 있는 가장 마지막 원소(밑바닥 가장 왼쪽 원소)와 교환
• 좌/우 자식 중 더 작은 원소와 교환

트라이

• 접두사 트리(prefix tree)

• n차 트리의 변종
• 각 노드에 문자를 저장하는 자료구조
  • 트리를 아래쪽으로 순회하면 단어 하나가 나온다.

• e.g. 유효한 단어 집합을 이용하는 문제
  • 접두사를 빠르게 찾아보기 위함 - 주어진 문자열이 유혀한지 아닌지 빠르게 확인
  • 길이가 $k$인 문자열이 주어졌을 때 $O(k)$ 시간에 해당 문자열이 유효한 접두사인지 확인 가능
  • 트리의 현재 노드를 참조값으로 넘겨서 접두어 반복 탐색 가능

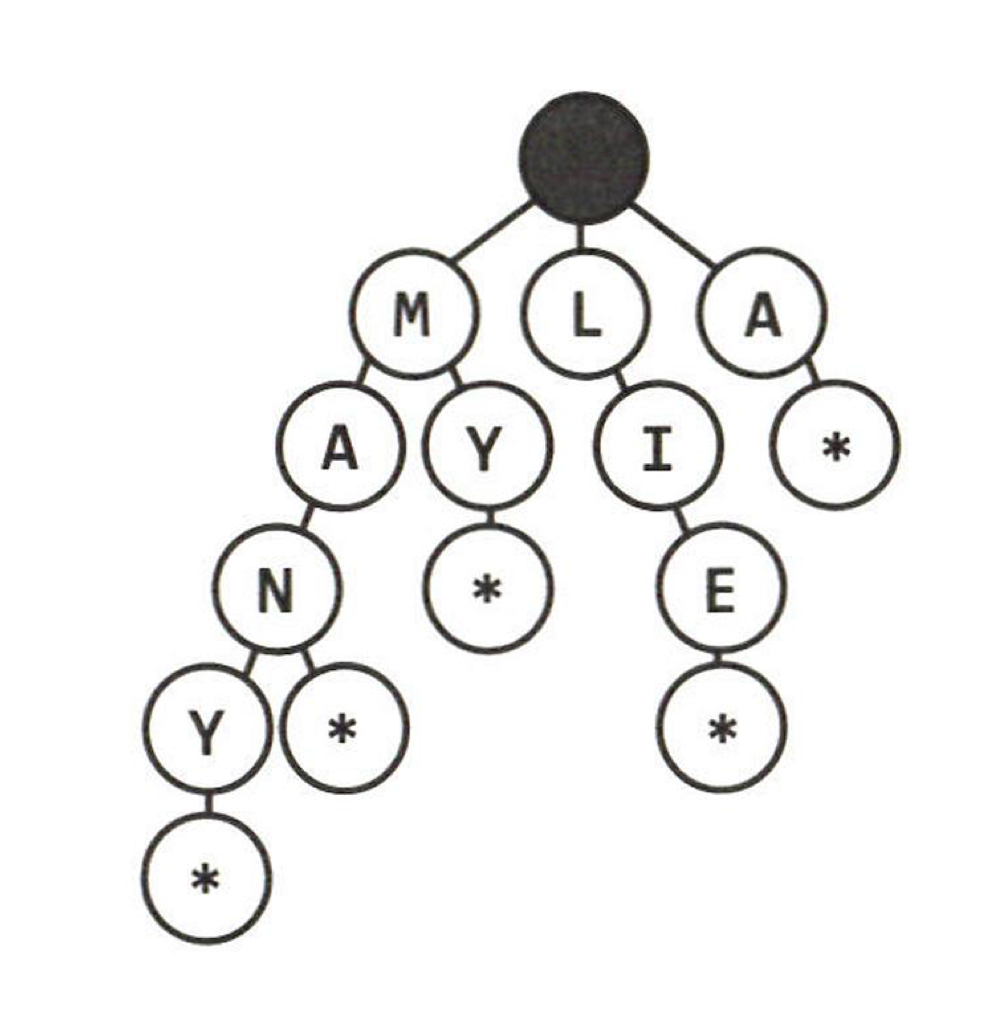
• 단어의 끝
  • Null node (* Node) 로 표현
    • 각 노드는 1 ~ {단어 길이 + 1} 개의 자식 노드를 가질 수 있음
  • 부모 노드 안에 boolean flag를 새로 정의해서 단어의 끝을 표현하기도 함
    • 각 노드는 0 ~ {단어 길이} 개의 자식 노드를 가질 수 있음

그래프

• $Tree ⊂ Graph$
• 트리 : 사이클이 없는 하나의 연결 그래프
• 그래프 : 단순히 노드와 그 노드를 연결하는 간선을 하나로 모아 놓은 것

• 그래프에는 방향성이 있을 수도 있고 없을 수도 있다.
• 그래프 : 부분 그래프로 구성 가능
  • 연결 그래프 : 모든 정점 쌍 간에 경로가 존재하는 그래프
  • 비순환 그래프 : 사이클이 없는 그래프

그래프 표현 방식

1. 인접 리스트

• 노든 정점을 인접 리스트에 저장
• 트리에서는 특정 노드(root) 다른 모든 노드로 접근 가능 But, 그래프는 특정 노드에서 다른 모든 노드로 접근 불가

class Graph {
  public Node[] nodes;
}

class Node {
  public String name;
  public Node[] children;
}

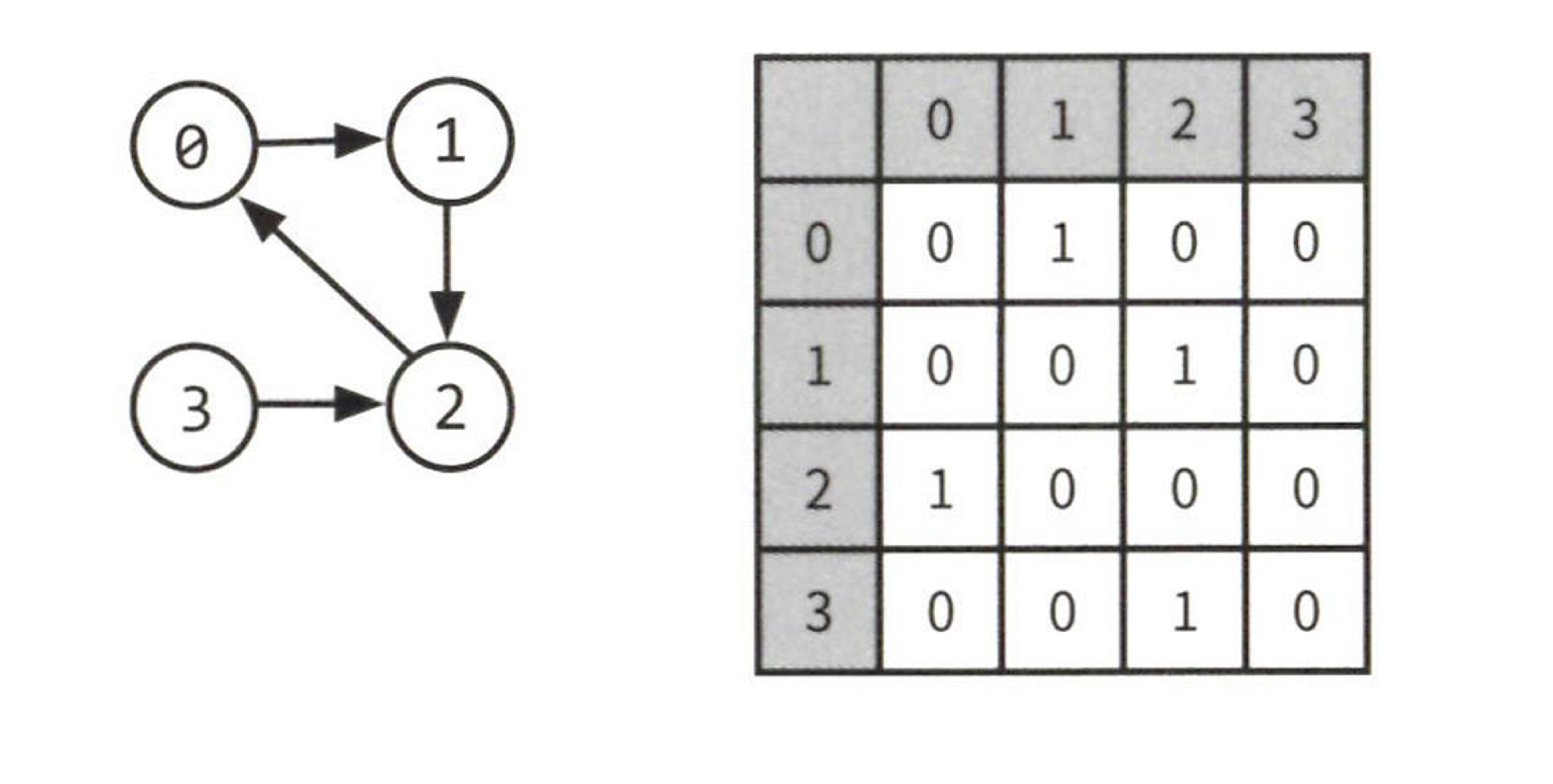
1. 인접 행렬

• N X N boolean matrix
• matrix[i][j] == true : i에서 j로의 간선 존재
• 무방향 그래프의 인접 행렬 형태 : 대칭 행렬(대각선을 기준으로)

그래프 탐색

1. 깊이 우선 탐색(DFS)

• 루트 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
• 넓게 탐색하기 전에 깊게 탐색
• 트리 순회는 모두 DFS의 한 종류
• 재귀적 동작
• e.g. 모든 노드 방문

void search(Node root){
  if (root == null) return;
  visit(root);
  for each(Node n in root.adjacent) {
    if (n.visited == false) {
      search(n);
    }
  }
}

1. 너비 우선 탐색(BFS)

• 루트 노드에서 시작해서 인접한 노드 먼저 탐색
• 깊게 탐색하기 전에 넓게 탐색
• 큐를 이용한 반복적 형태
• e.g. 두 노드 사이 최단/임의 경로 탐색

void search(Node root) {
  Queue queue = new Queue();
  root.marked = true;
  queue.enqueue(root);

  while (!queue.isEmpty()) {
    Node r = queue.dequeue();
    visit(r);
    foreach (Node n in r.adjacent) {
      if (n.marked == false) {
        n.marked = true;
        queue.enqueue(n);
      }
    }
  }
}

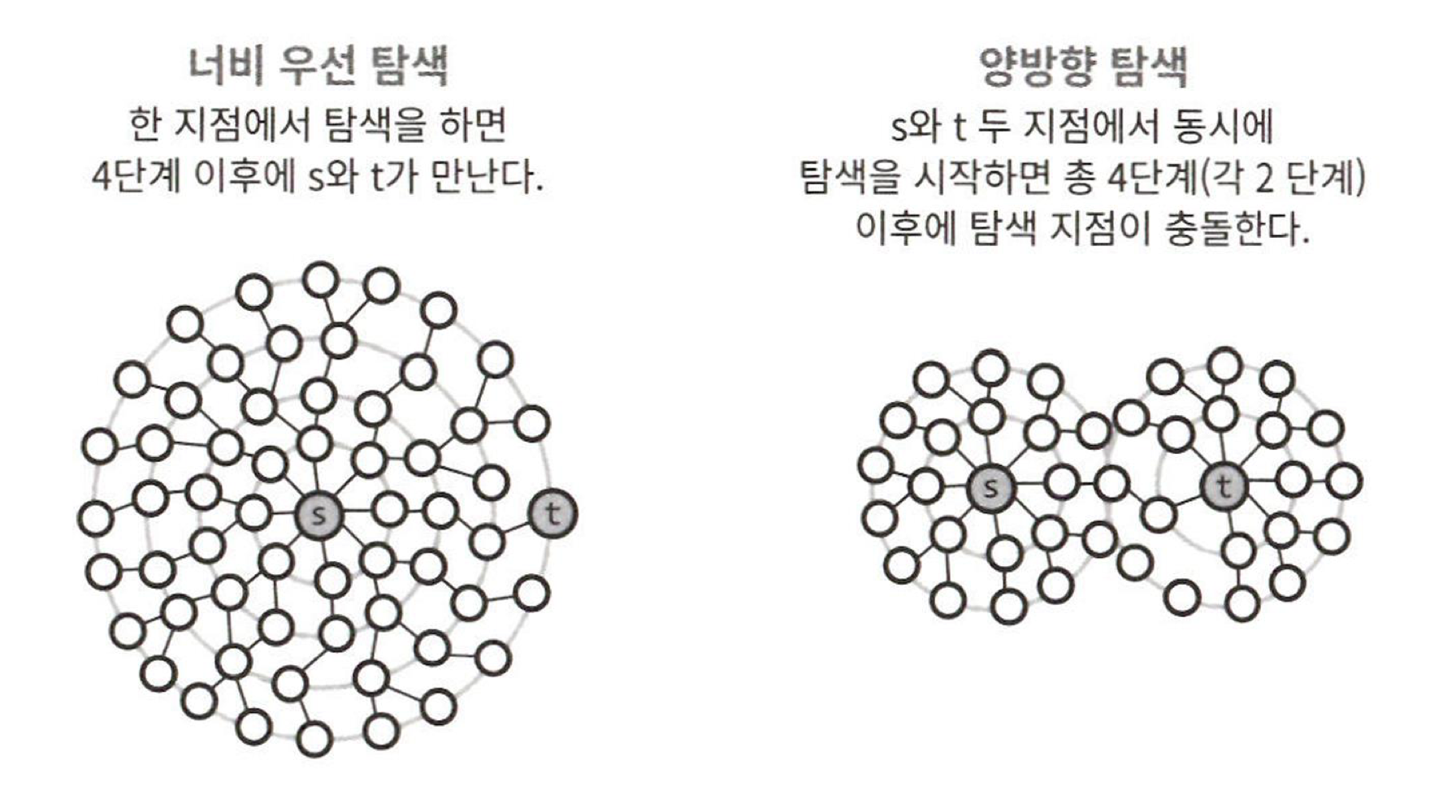
양방향 탐색

• 출발지와 도착지 두 노드에서 동시에 너비 우선 탐색 수행 후, 두 탐색 지점이 충돌하는 경우 경로 탐색
• 전통적인 너비 우선 탐색 : $O(k^d)$
• 양방향 탐색 : $O(k^{d/2})$