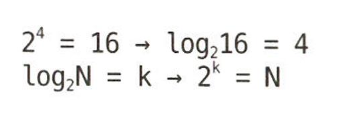🦊 1. Big-O Notation

들어가며

Big - O : 알고리즘의 효율성을 나타내는 지표 혹은 언어

시간 복잡도

점근적 실행 시간, 혹은 Big - O 시간에 대한 개념이다

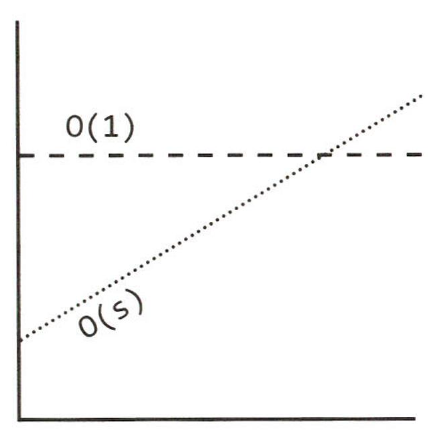
O(s) : 온라인 전송

파일 크기가 커짐에 따라 전송 시간이 선형적으로 증가

O(1) : 비행기로 직접 전송

파일 크기에 관계 없이 상수 시간만큼 소요

s 가 점차 커지다보면 O(1) 을 넘는 순간이 온다.

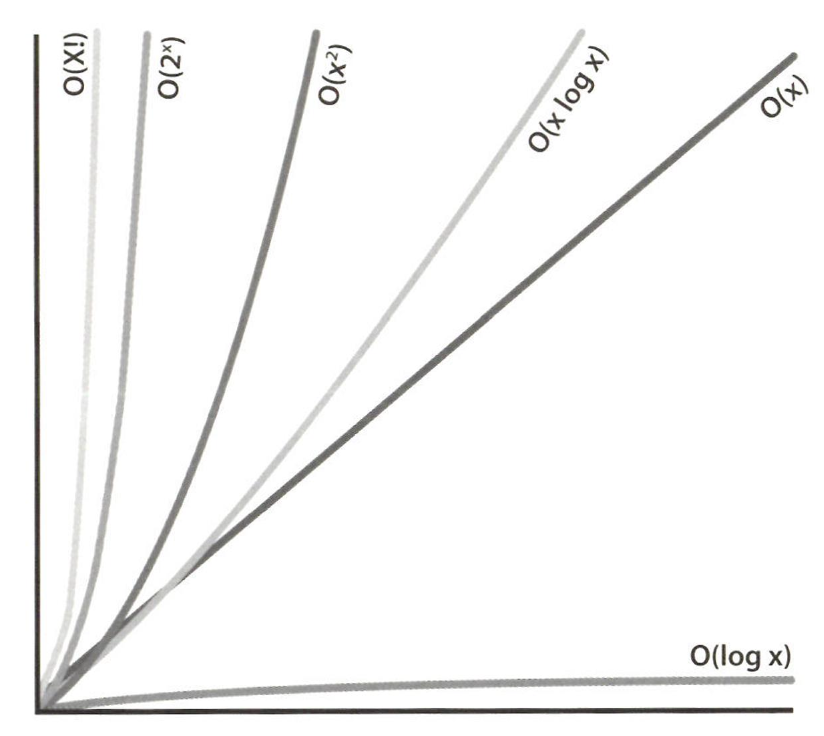
big-O, big-Θ, big-Ω

O : 시간의 상한을 나타낸다. 예를 들면 배열의 모든 값을 출력하는 알고리즘은 O(N) 으로 표현할 수 있다.

Ω : 등가 개념 혹은 시간의 하한을 나타낸다.

Θ : O 와 Ω 를 둘 다 의미한다. 어떤 알고리즘의 수행 시간이 O(N) 이자 Ω(N) 이라면 수행 시간은 Θ(N) 으로 나타낼 수 있다.

최선의 경우, 최악의 경우, 평균적인 경우

퀵 정렬을 통한 예시를 확인해보자.

• 최선의 경우 : 만약 모든 원소가 동일하다면 한 번 순회하고 끝나기 때문에 수행 시간을 O(N) 이라고 할 수 있다.
• 최악의 경우 : 배열이 역순으로 정렬되어 있고 부분 배열의 첫 원소를 항상 축으로 잡는다면 수행 시간은 O(N^2) 이라고 할 수 있다.
• 평균적인 경우 : 최선, 최악의 경우는 자주 발생하지 않기 때문에 평균적으로 O(NlogN) 이라고 할 수 있다.

공간복잡도

알고리즘에서는 시간 뿐만 아니라 메모리 공간도 신경을 써야 한다.

공간 복잡도는 시간 복잡도와 평행선을 달리는 개념이다.

예를 들어 크기 N인 배열을 만드는데 O(N) 의 공간이 필요하다.

재귀 호출에서 사용하는 스택 공간도 공간 복잡도 계산에 포함된다.

이 함수는 호출될 때마다 스택의 깊이가 깊어지기 때문에 O(N) 공간을 사용한다.

이 코드는 함수를 대략 n 번 실행했지만 호출 스택에 동시에 존재하지 않기 때문에 O(1) 공간을 사용한다.

상수항은 무시하라

O(2N) 으로 표기되어야 할 알고리즘은 실제로 O(N) 으로 표현한다.

지배적이지 않은 항은 무시하라

앞서 상수항은 무시해도 된다고 언급했다.

따라서 O(N^2 + N^2) 은 O(N^2) 가 된다.

여러 부분으로 이루어진 알고리즘: 덧셈 vs 곱셈

어떤 알고리즘이 두 단계로 이루어져 있다고 할 때, 어떤 경우에 수행시간을 더하고 곱해야 할까

왼쪽에선 A 일을 한 뒤에 B 일을 하기 때문에 수행시간은 O(A+B) 이다

오른쪽에선 A의 각 원소에 대해 B 일을 수행하기 때문에 수행시간은 O(AB) 이다

즉, 만약 알고리즘이 A 일을 모두 끝마친 후 B 일을 수행하라는 형태라면 A + B 여야 한다.

만약 알고리즘이 A 일을 할때마다 B 일을 수행해야 한다면 A * B 여야 한다.

상환시간

ArrayList 는 원소 삽입 시 필요에 따라 배열 크기를 조절하는 자료구조이다.

배열에 가용 공간이 존재하면 삽입 연산의 수행시간은 O(1) 이다

배열이 가득 차 있을 때 삽입하려면 배열의 크기를 2N 으로 새로 조절하고 모든 원소를 복사해야 하므로 수행시간은 O(N) 이다

하지만 최악의 경우인 O(N) 은 자주 발생하지 않기 때문에 수행시간을 분할 상환해야 한다.

따라서 X 개의 원소를 삽입하는데 걸리는 시간은 O(2X) → O(1) 이다

log N 수행시간

이진 탐색과 균형 이진 탐색 트리의 원소를 찾는 수행 시간은 O(log N) 이다.

처음에는 원소 N개가 들어있는 배열에서 시작하고 한 단계마다 탐색할 원소의 개수가 N/2 로 줄어든다.

반대로 생각하면 2를 몇 번 곱해야 N이 되는가?

즉, 2^k = N 을 만족하는 k 는 무엇인가? 바로 로그라고 할 수 있다

재귀적으로 수행 시간 구하기

이 함수의 시간 복잡도는 O(N^2) 이 아니다.

수행 시간을 추측하지 말고 코드를 하나씩 읽어봐야 한다.

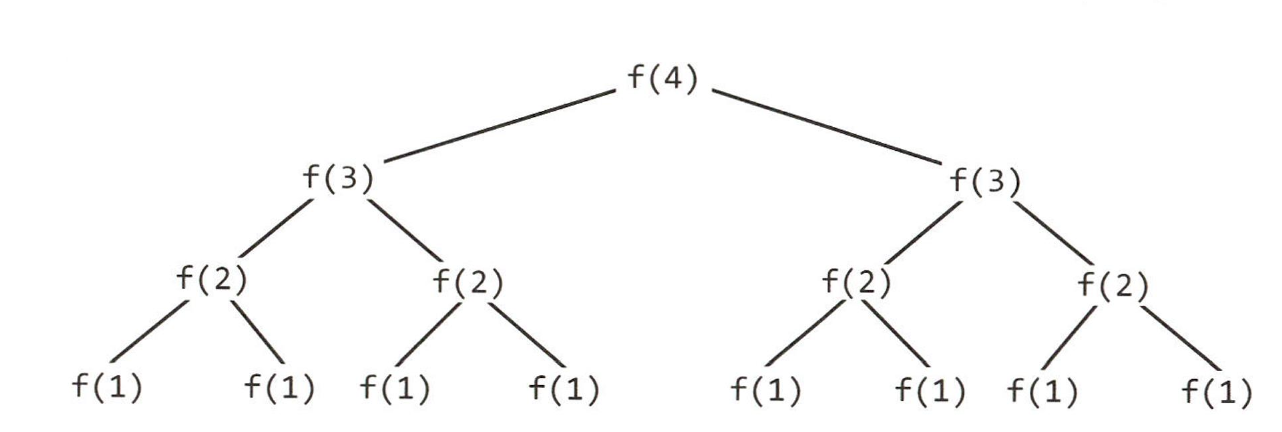
트리의 깊이가 N 이고 각 노드는 두 개의 자식 노드를 가지고 있다.

따라서 깊이가 한 단계 깊어질 때 마다 두 배 많은 노드를 호출하게 된다.

따라서 전체 노드의 갯수는 2^(N-1) - 1 이 된다.

그래서 보통 재귀 함수의 수행시간은 O(분기^깊이) 가 된다.

결론적으로 위 함수의 수행 시간은 O(2^N) 이 된다.

공간 복잡도는 O(N) 이다.

전체 노드의 갯수는 O(2^N) 개 이지만 특정 시각에 사용하는 공간의 크기는 O(N) 이다.