🦊 4. Trees and Graphs

4. Trees and Graphs

트리의 종류

트리는 노드로 이루어진 자료구조이다.

• 트리는 하나의 루트 노드를 갖는다.
• 루트 노드는 0개 이상의 자식 노드를 가진다.
• 그 자식 노드 또한 0개 이상의 자식 노드를 가지며 이는 반복적으로 정의된다.

트리에는 사이클이 존재할 수 없다.

노드들은 특정 순서로 나열될 수도 있고 그렇지 않을 수도 있다.

각 노드는 어떠한 자료형으로도 표현 가능하다.

각 노드는 부모 노드로의 연결이 있을 수도 있고 없을 수도 있다.

Class Node {
	public String name;
	public Node[] children;
}

이 노드 클래스를 포함하는 Tree 클래스를 정의할 수도 있다.

면접 문제에서는 일반적은 Tree 클래스를 사용하지 않는다.

트리 및 그래프 문제들은 대부분 세부사항이 모호하거나 가정 자체가 틀린 경우가 많다.

다음 이슈들에 유의하고 필요하면 명확하게 해 줄 것을 요구하자.

트리 vs 이진 트리

이진 트리는 각 노드가 최대 두 개의 자식을 갖는 트리이다.

모든 트리가 이진 트리는 아니다.

종종 이진 트리가 아닌 트리를 다뤄야 한다.

예를 들어 전화번호를 표혈할 때 트리를 사용한다고 가정하면,

각 노드가 10개의 자식 (0 ~ 9)을 갖는 10차 트리를 사용해야 한다.

자식이 없는 노드는 말단 노드 라고 부른다.

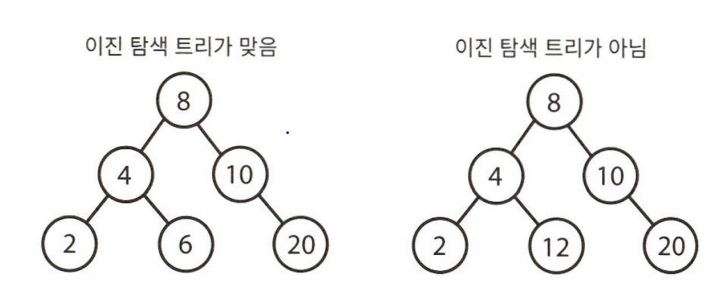
이진 트리 vs 이진 탐색 트리

이진 탐색 트리는 모든 노드가 다음 조건을 만족하는 트리이다.

'모든 왼쪽 자식들 <= n < '모든 오른쪽 자식들' 속성이 모든 노드 n에 대해 반드시 참이다.

다음 왼쪽 트리는 이진 탐색 트리이지만 오른쪽은 12가 8의 왼쪽에 있기 때문에 이진 탐색 트리가 아니다.

균형 vs 비균형

균형 트리의 일반적인 유형으로는 레드-블랙트리와 AVL 트리가 있다.

많은 트리가 균형 잡혀 있긴 하지만 전부 그런 것은 아니다.

균형을 잡는다는 것이 왼쪽과 오른쪽 부분 트리의 크기가 완전히 같게 하는 것을 의미하지는 않는다.

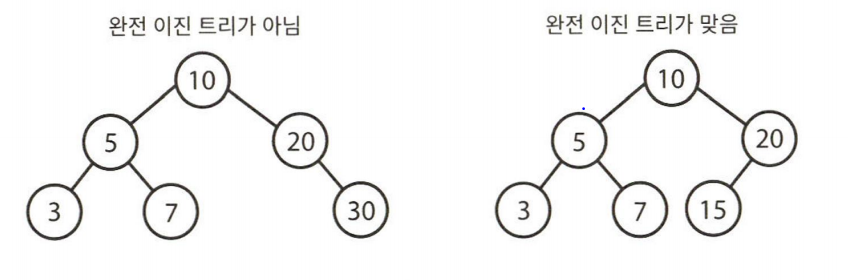
완전 이진 트리

완전 이진 트리는 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리이다.

마지막 레벨이 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 순차적으로 채워져야 한다.

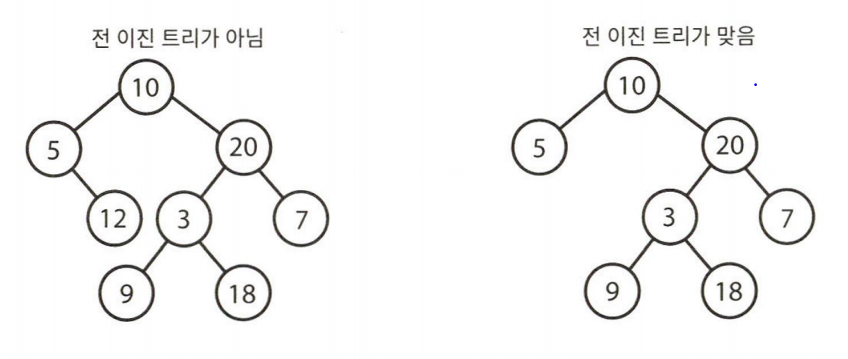
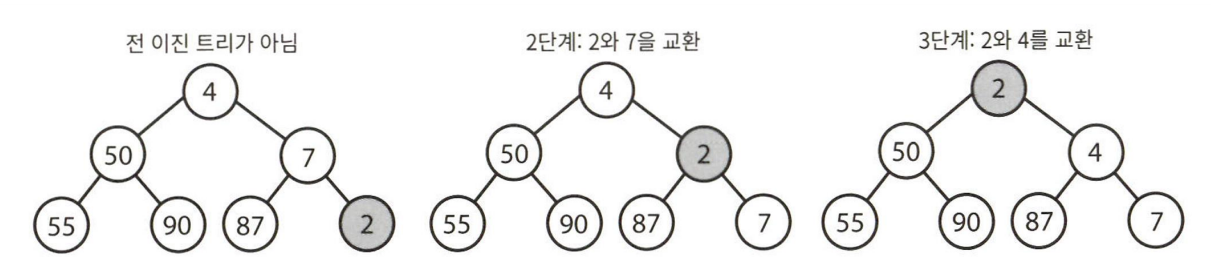
전 이진 트리

전 이진 트리는 모든 노드의 자식이 없거나 정확히 두 개 있는 경우를 말한다.

자식이 하나만 있는 노드가 존재해서는 안 된다.

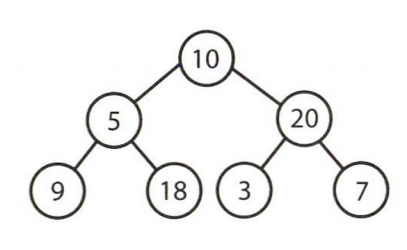
포화 이진 트리

포화 이진 트리는 전 이진 트리이면서 완전 이진 틀인 경우를 말한다.

모든 말단 노드가 같은 레벨에 있고 마지막 레벨의 노드의 개수가 최대이어야 한다.

이진 트리 순회

중위 순회

중위순회(in-order traversal)는 왼쪽 가지 → 현재 → 오른쪽 가지 순서로 노드를 방문한다.

이진 탐색 트리를 중위 순회하면 오름차순으로 방문하게 된다.

void inOrderTraversal(TreeNode node) {
	if (node != null) {
		inOrderTraversal(node.left);
		visit(node);
		inOrderTraversal(node.right);
	}
}

전위 순회

전위순회(pre-order traversal)은 자식 노드보다 현재 노드를 먼저 방문하는 방법이다.

가장 먼저 방문하게 되는 노드는 언제나 루트이다.

void preOrderTraversal(TreeNode node) {
	if (node != null) {
		visit(node);
		preOrderTraversal(node.left);
		preOrderTraversal(node.right);
	}
}

후위 순회

후위순회(post-order traversal)는 모든 자식 노드들을 먼저 방문한 뒤 마지막에 현재 노드를 방문하는 방법을 말한다.

가장 마지막에 방문하게 될 노드는 항상 루트이다.

void postOrderTraversal(TreeNode node) {
	if (node != null) {
		postOrderTraversal(node.left);
		postOrderTraversal(node.right);
		visit(node);
	}
}

이진 힙(최소힙과 최대힙)

최소힙은 트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있다는 점에서 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다는 특성이 있다.

따라서 루트는 트리 전체에서 가장 작은 원소이다.

삽입

최소힙에 원소를 삽입할 때 언제나 트리의 밑바닥에서 삽입을 시작한다.

새로운 원소는 완전 트리의 속성에 위배되지 않도록 밑바닥 가장 오른쪽으로 삽입된다.

이후 제대로 된 자리를 찾을 때까지 부모 노드와 교환해 나가며

최소 원소를 위쪽으로 올린다.

힙에 있는 노드의 개수를 n이라 할 때 이 연산은 O(log N) 시간이 걸린다.

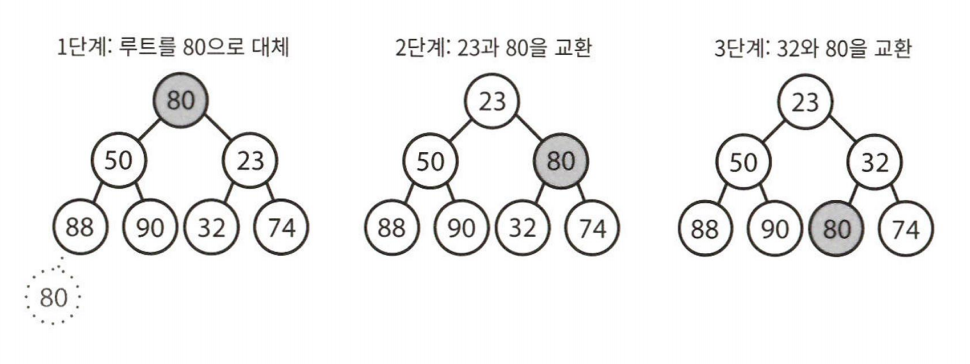
최소 원소 뽑아내기

최소 원소는 언제나 가장 위에 놓인다.

힙에서 어떻게 제거하느냐가 까다로운 부분이다.

최소 원소를 제거한 후에 힙에 있는 가장 마지막 원소와 교환한다.

그 다음 최소힙의 성질을 만족하도록 해당 노드를 자식 노드와 교환해 나감으로써 밑으로 보낸다.

이 알고리즘도 O(log N) 시간이 걸린다.

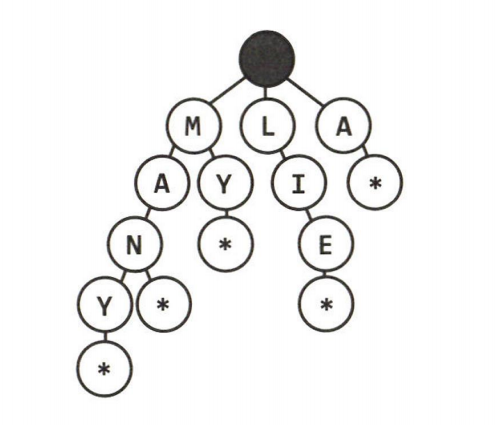
트라이

접두사 트리 (prefix tree) 라고도 불린다.

트라이는 N차 트리의 변종으로 각 노드에 문자를 저장하는 자료구조이다.

따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다.

* 노드(Null Node)는 종종 단어의 끝에 나타나서 단어가 완성되었음을 알린다.

접두사를 빠르게 찾아보기 위한 아주 흔한 방식으로 모든 언어를 트라이에 저장하는 방식이 있다.

트라이를 이용하면 아주 빠르게 확인 가능하다.

트라이는 길이가 K 인 문자열이 주어졌을 때 O(K) 시간에 해당 문자열이 유효한 접두사인지 확인할 수 있다.

그래프

트리는 그래프의 한 종류이다.

하지만 모든 그래프가 트리는 아니다.

트리는 사이클이 없는 하나의 연결 그래프이다.

그래프는 단순히 노드와 그 노드를 연결하는 간선(edge)를 하나로 모아놓은 것과 같다.

• 그래프는 방향성이 있을 수도 있고 없을 수도 있다.
• 그래프는 여러 고립된 부분 그래프로 구성될 수 있다. 모든 정점 쌍 간에 경로가 존재하는 그래프는 연결 그래프 라고 부른다.
• 그래프에는 사이클이 있을 수도 있고 없을 수도 있다. 사이클이 없는 그래프는 비순환 그래프 라고 부른다.

인접 리스트

인접 리스트(adjacency list)는 그래프를 표현할 때 사용되는 가장 일반적인 방법이다.

모든 정점을 인접 리스트에 저장한다.

무방향 그래프는 (a, b) 간선이 두 번 저장된다.

Class Graph {
	public Node[] nodes;
}

Class Node {
	public String name;
	public Node[] children;
}

그래프는 트리와 달리 특정 노드에서 다른 모든 노드로 접근이 가능하지는 않아 Graph 라는 클래스를 사용한다.

배열, 해시테이블과 각 인덱스마다 존재하는 또 다른 리스트를 이용해 인접 리스트를 표현할 수 있다.

0: 1
1: 2
2: 0, 3
3: 2
4: 6
5: 4
6: 5

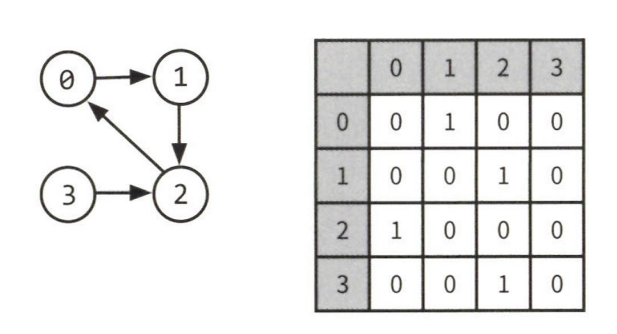
인접 행렬

인접 행렬은 NxN 불린 행렬로써 matrix[i][j] == true 이면 i -> j 간선이 있다는 것이다.

인접 행렬은 조금 효율성이 떨어진다.

어떤 노드에 인접한 노드를 찾기 위해서 모든 노드를 전부 순회해야 할 수 있다.

그래프 탐색

깊이 우선 탐색(DFS)는 루트 노드에서 시작해서 다음 분기로 넘거가기 전에 해당 분기를 완벽하게 탐색하는 방법이다.

너비 우선 탐색(BFS)는 루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법이다.

DFS는 그래프에서 모든 노드를 방문하고자 할 때 선호되는 편이다.

BFS는 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 일반적이다.

깊이 우선 탐색(DFS)

트리의 순회와 그래프 탐색의 가장 큰 차이는 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다는 것이다.

그렇지 않을 경우 무한루프에 빠질 위험이 있다.

void search(Node root) {
	if (root == null) return;
	visit(root);
	root.visited = true;
	for each (Node n in root.adjacent) {
		if (n.visited == false) {
			search(n);
		}
	}
}

너비 우선 탐색(BFS)

BFS 는 재귀적으로 동작하지 않고 큐를 사용한다.

void search(Node root) {
	Queue queue = new Queue();
	root.marked = true;
	queue.enqueue(root);

	while (!queue.isEmpty()) {
		Node r = queue.dequeue();
		visit(r);
		foreach (Node n in r.adjacent) {
			if (n.marked == false) {
				n.marked = true;
				queue.enqueue(n);
			}
		}
	}
}

양방향 탐색

양방향 탐색은 출발지와 도착지 사이에 최단 경로를 찾을 때 사용되곤 한다.

기본적으로 출발지와 도착지 두 노드에서 동시에 너비 우선 탐색을 수행한 뒤, 두 탐색 지점이 충돌하는 경우에 경로를 찾는 방식이다.

모든 노드가 적어도 k개의 이웃 노드와 연결되어 있고 s → t로의 최단 거리가 d가 되는 그래프를 생각해보자.

• 전통적인 BFS 에서는 레벨마다 k 개의 노드를 탐색해야 하므로 d번 반복하면 O(K^d) 개의 노드를 탐색한다.
• 양방향 탐색을 사용한다면 대략 d/2 단계까지 탐색한 후 충돌한다. 따라서 s 와 t 각각에서 방문할 노드는 k^(d/2) 개가 될 것이고 전체 방문할 노드는 대략 2*k^(d/2) 개가 된다.

즉, 양방향 탐색은 BFS 보다 적어도 k^(d/2) 만큼 빠르다.

다른 방식으로 말하면 2배 더 긴 경로까지 찾을 수 있다!