🐢 1. Big-O Notation

💡 Big O(빅-오) 표기법 : O(N)

알고리즘 최악의 실행 시간을 표기

아무리 최악의 상황에도, 이정도 성능은 보장한다는 의미

Ω (오메가) 표기법 : Ω(N)

알고리즘 최상의 실행 시간을 표기

Θ(세타) 표기법 : Θ(N)

알고리즘 평균 실행 시간을 표기

시간 복잡도 : 알고리즘의 실행 속도

공간 복잡도 : 알고리즘이 실행될 때 메모리를 얼마나 사용하는가

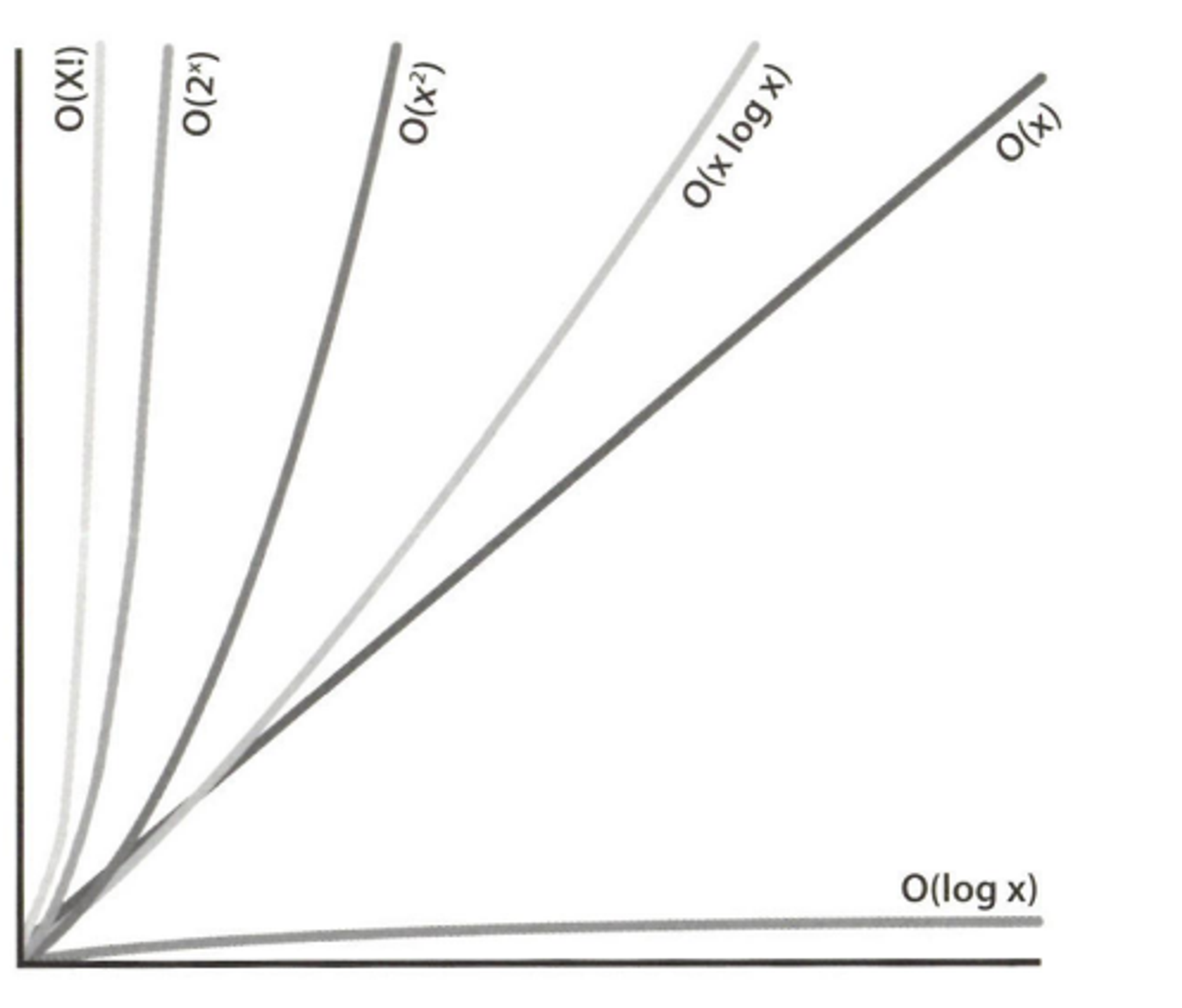
빅오 표기법 : 시간 복잡도를 나타내는 표기법

---

🫧 비유하기

파일 크기가 작다면 ? 온라인으로 전송

파일 크기가 무지막하게 크다면 ? 운전 or 비행기🚀

🫧 시간 복잡도

점근적 실행 시간 (asymptotic runtime), big-O 시간 개념

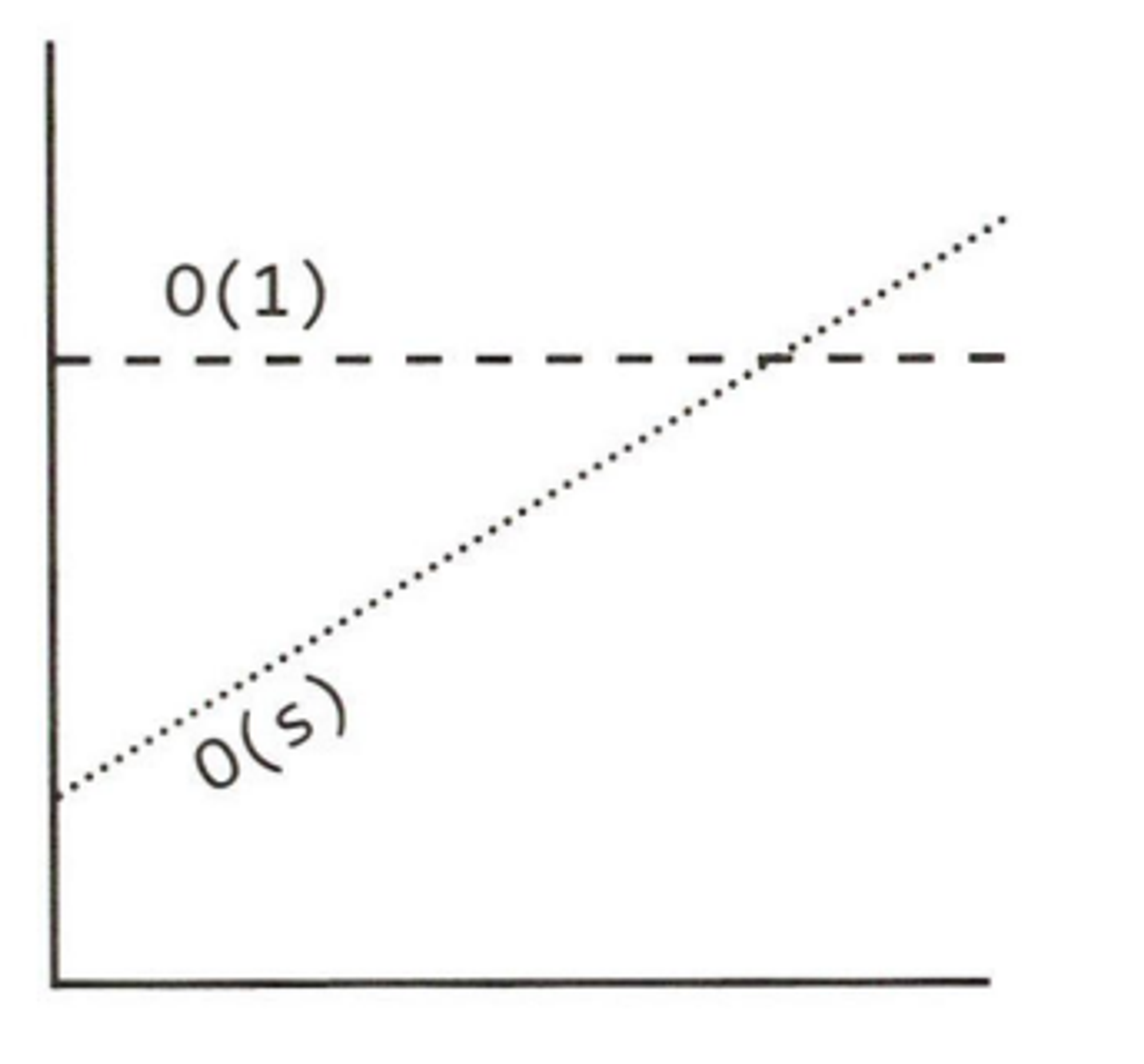
• 온라인 전송 : O(s), s는 파일의 크기
  • 파일의 크기가 증가함에 따라 전송 시간이 선형적으로 증가
• 비행기 전송 : 파일의 크기 상관없이 O(1)
  • 상수시간만큼 소요

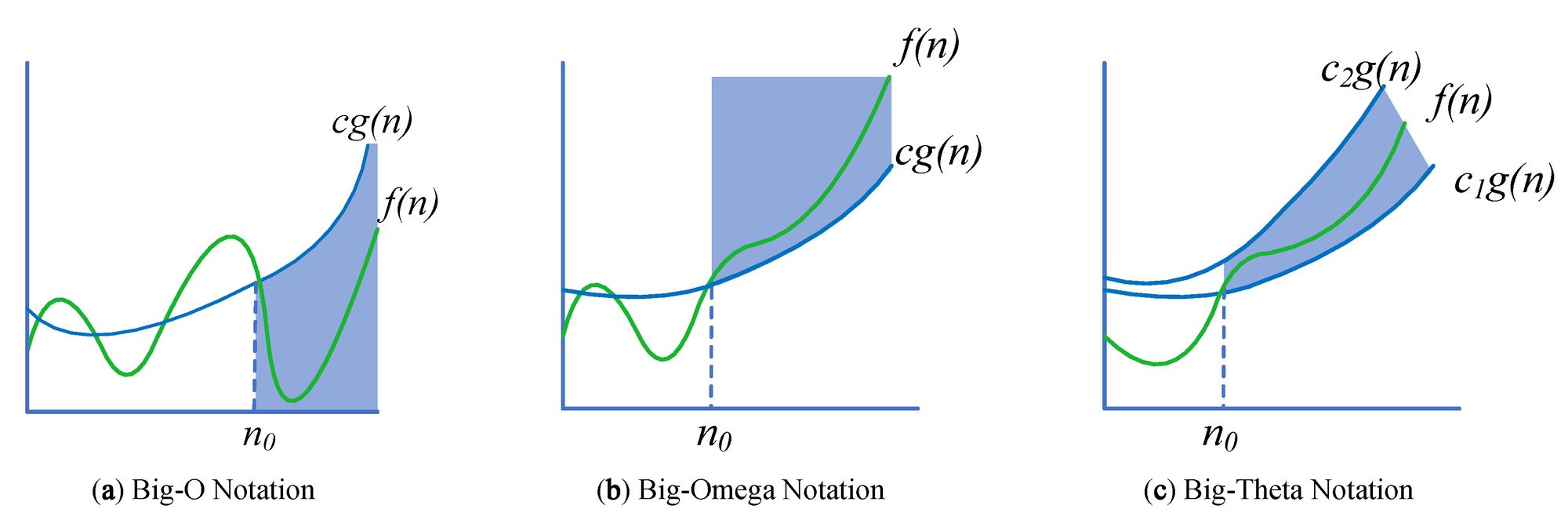
❤️ big-O

시간의 상한

배열의 모든 값을 출력하는 알고리즘

O(n) 뿐만 아니라, O(n^3) 혹은 O(n) 보다 큰 어떤 수행 시간으로 가능

❤️ big-Ω (omega)

등가 or 하한

Ω(n) 뿐만 아니라, Ω(log N) 혹은 Ω(1) 로 표현 가능

❤️ big-θ (theta)

: O와 Ω 둘 다 의미 (딱 맞는 수행 시간)

O(n) 이면서 Ω(n) 이라면, 수행 시간은 θ(n) 로 표현 가능

🔎 퀵 정렬 관점
”축”이 되는 원소 하나를 무작위로 뽑은 뒤, 이보다 작은 원소들은 앞에, 큰 원소들은 뒤에 놓이도록 한다
그 결과, 부분 정렬 완성되고 왼쪽 오른쪽 부분을 이와 비슷하게 재귀적으로 정렬한다

🧡 최선의 경우

모든 원소가 동일하다면 단순히 배열을 한차례 순회하고 끝

수행 시간은 O(n)

🧡 최악의 경우

배열에서 가장 큰 원소가 축이 된다면, 절반 크기가 아닌 고작 하나 줄어든 크기의 부분 배열로 나뉘게 된다

수행 시간은 O(n^2)

🧡 평균의 경우

수행 시간은 O(nlogn)

🫧 공간 복잡도

: 메모리 or 공간

🫧 상수항은 무시하라

: 단순히 증가 비율을 나타내므로, 상수항 무시하기

🫧 지배적이지 않은 항은 무시하라

: 최고차항 보다 작은 항들은 무시해도 된다

ex) O(n^2 + n) 은 O(n^2)

🫧 여러 부분으로 이루어진 알고리즘: 덧셈 vs 곱셈

: 알고리즘이 “A 끝난 후 B 수행하라” → A + B

알고리즘이 “A 할 때 B 수행하라” → A * B

🫧 상환 시간

: ArrayList 는 배열의 역할 + 크기가 자유로운 자료구조

x개의 원소를 삽입했을 때 필요 시간은 O(2x), 분할 상환해서 삽입 한번에 필요한 시간은 O(1)

🫧 log N 수행 시간

: 이진 탐색(binary search) 는 n개의 정렬된 원소가 들어 있는 배열에서 원소 x를 찾을 때 사용

• 먼저 원소 x와 배열의 중값을 비교
  • x === 중간값 만족하면 반환
  • x < 중간값 만족하면 배열의 왼쪽 재탐색
  • x > 중간값 만족하면 배열의 오른쪽 재탐색
• 원소 n개의 배열에서 시작
  • 한 단계 지날 수록 n/2개, n/4개로 줄어든다

: 2^k = n 에서 k는 log(n)

원소의 개수라 절반씩 줄어든다면 그 문제의 실행 시간은 O(log n)

균형 이진 탐색 트리 (balanced binary search tree) 에서도 O(log n)

매 단계마다 원소의 대소를 비교한 뒤 왼쪽 혹은 오른쪽으로 내려감

각 단계에서 검색해야 할 노드의 개수가 절반씩 줄어드므로, 문제 공간 또한 절반씩 줄어듦

🫧 재귀적으로 수행 시간 구하기

: 다수의 호출로 이루어진 재귀 함수에서 수행 시간은 O(분기^깊이)로 표현

분기(branch)란 재귀 함수가 자신을 재호출하는 횟수

🫧 예제 및 연습 문제

💛 예제 1

➡️ O(n)

void foo(int[] array) {
	int sum = 0;
	int product = 1;
	
	for (int i = 0; i < array.length; i++) {
		sum+= array[i];
	}

	for (int i = 0; i < array.length; i++) {
		product *= array[i];
	}

	System.out.println(sum + ", " + product);
}

💛 예제 2

➡️ O(n^2)

void printPairs(int[] array) {
	for (int i = 0; i < array.length; i++) {
		for (int j = 0; j < array.length; j++) {
			System.out.println(array[i] + ", " + array[j]);
		}
	}
}

💛 예제 3

➡️ O(n^2)

void printUnorderedPairs(int[] array) {
	for (int i = 0; i < array.length; i++) {
		for (int j = i + 1; j < array.length; j++) {
			System.out.println(array[i] + ", " + array[j]);
		}
	}
}

💛 예제 4

➡️ O(ab)

void printUnorderedPairs(int[] arrayA, int[] arrayB) {
	for (int i = 0; i < arrayA.length; i++) {
		for (int j = 0; j < arrayB.length; j++) {
			if (arrayA[i] < arrayB[i]) {
				System.out.println(arrayA[i] + ", " + arrayB[j]);
			}
		}
	}
}