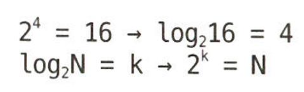🐹 1. Big-O Notation

big-O: 알고리즘의 효율성을 나타내는 지표 혹은 언어

[ 비유하기 ]

디스크에 있는 파일을 다른 지역에 사는 친구에게 가장 빨리 보낼 수 있는 방법은 무엇일까?

이메일, FTP, 다른 온라인을 통한 전송 방법을 대부분 생각할 것

→ 파일 크기에 따라 생각해보아야 함

1) 파일 크기가 작은 경우

→ 당연히 온라인 전송이 빠를 것이다.

미국에 있는 친구에게 직접 전달한다면 공항으로 가서 비행기에 오른 뒤 친구가 있는 곳까지 날아가야 함. 5-10시간 소요

2) 파일의 크기가 큰 경우

→ 비행기를 통해 물리적으로 배달하는 것이 더 빠를 수 있다.

1TB 크기의 파일을 온라인을 통해 전송하려 한다면 하루 이상이 걸릴 수 있다. 정말 급한 상황이라면 비행기를 타는 것이 나을지도 모른다.

[ 시간 복잡도 ]

위의 예제 데이터 전송 ‘알고리즘’의 실행시간

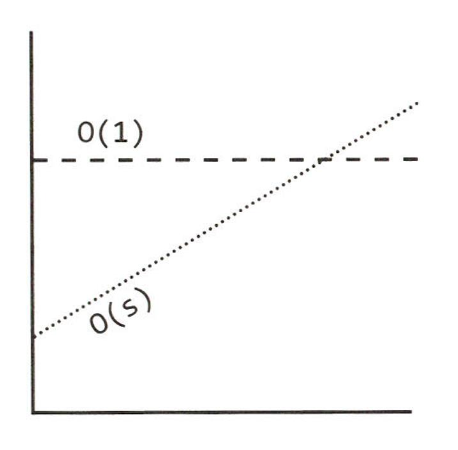
• 온라인 전송: O(s) (s: 파일 크기)

  → 파일의 크기가 증가함에 따라 전송 시간 또한 선형적으로 증가

• 비행기를 통한 전송: 파일 크기에 관계없이 O(1)

  → 파일의 크기가 증가한다고 해서 친구에게 파일을 전송하는 데 걸리는 시간이 늘어나지 않는다. 즉, 상수 시간만큼 소요된다.

big-O, big-Θ, big-Ω(학계)

• O(big-O): 알고리즘 수행 시간의 상한, ‘작거나 같은’ 부등호
• Ω(big-Omega): 등가 개념 혹은 하한, Ω 수행 시간보다 빠를 수 없음
• Θ(big theta): O와 Ω 둘 다를 의미. 어떤 알고리즘의 수행이 O(N)이면서 Ω(N)이라면 Θ(N)으로 표현 가능

길이 N의 배열 출력을 표기할 때는 O(N) 말고도 O(N^2), O(N^3) 등으로 표현 가능하지만 실제로 우리는 Θ를 사용하는 것처럼 O(N)이라고 표현한다.

최선의 경우, 최악의 경우, 평균적인 경우(실제)

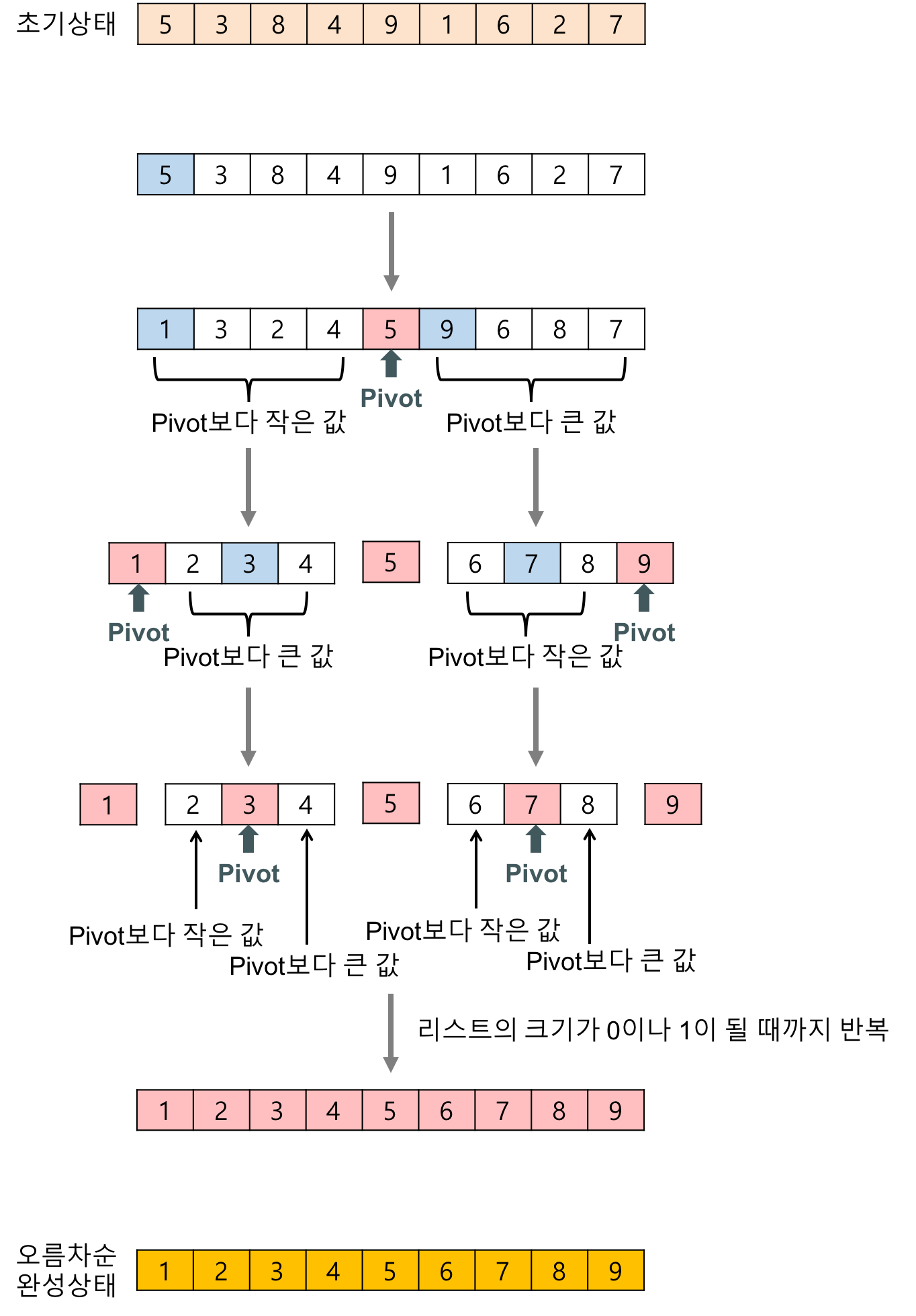
퀵 정렬(quick sort)의 관점에서 각 경우를 바라보자

• 최선의 경우: O(N)

  모든 원소가 동일하다면 퀵 정렬은 평균적으로 단순히 배열을 한 차례 순회하고 끝날 것이다.

  혹은 배열이 이미 정렬되어 있어도 마찬가지이다.

• 최악의 경우: O(N^2)

  운이 없게 배열에서 가장 큰 원소가 계속해서 축이 된다면(ex.배열이 역순으로 정렬되어 있고 축을 항상 첫 번째 원소로 지정) 재귀 호출이 배열을 절반 크기의 부분 배열로 나누지 못하고, 고작 하나 줄어든 크기의 부분 배열로 나누게 된다.

• 평균적인 경우: O(NlogN)

알고리즘에서 최악의 경우와 평균적인 경우가 대부분 같지만, 가끔 달라서 둘 다 언급해야 할 때도 있다.

[ 공간 복잡도 ]

크기가 n인 배열을 만들고자 한다면 O(n)의 공간 필요

공간 복잡도 예시

• 재귀호출 스택 공간: O(n)

    int sum(int n) { /* 예제 1 */
    		if (n <= 0)
    				return 0;
    		}
    		return n + sum(n-1);
    }
  

  호출될 때마다 스택의 깊이는 깊어진다.

    sum(4)
    	-> sum(3)
    			-> sum(2)
    					-> sum(1)
    							-> sum(0)
  

  위의 호출은 전부 스택에 더해지고 실제 메모리 공간을 잡아 먹는다.

• 0과 n 사이에서 인접한 두 원소의 합 구하기: O(1)

    int pairSumSequence(int n) { /* 예제 2 */
    		int sum = 0;
    		for (int i = 0; i < n; i++) {
    				sum += pairSum(i, i + 1);
    		}
    		return sum;
    }
      
    int pairSum(int a, int b) {
    		return a + b;
    }
  

  위 코드는 pairSum 함수를 대략 O(n)번 호출했지만, 이 함수들이 호출 스택에 동시에 존재하지 않으므로 O(1) 공간만 사용한다.

[ 상수항은 무시하라 ]

두 개의 중첩되지 않은 루프로 이루어진 코드를 O(2N)이 아닌 O(N)으로 표기한다.

O(2N)이 더 정확하지 않은 가에 대한 반대 예시를 아래에서 보여준다.

최소와 최대 1

int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int x: array) {
		if (x < min) min = x;
		if (x > max) max = x;
}

최소와 최대 2

int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int x : array) {
		if (x < min) min = x;
}
for (int x : array) {
		if (x > max) max = x;
}

1번 예시와 2번 예시 중 for문을 한 번만 사용한 1번 예제가 더 빠른가?

자세히 파악할 필요는 없지만 big-O 표기법은 수행 시간이 어떻게 변화하는 지를 표현하는 도구이다. 따라서 O(2N)이 언제나 O(N)보다 나은 것은 아니라는 사실만 받아들이면 된다.

[ 지배적이지 않은 항은 무시하라 ]

O(N^2 + N)과 같은 수식이 있을 때 N은 상수항은 아니지만 특별히 중요한 항은 아니다.

O(N^2 + N^2)은 이전에 상수항을 무시하라 하였으므로 O(N^2)이 된다. 그렇다면 뒤의 N^2항을 무시한 것이다. → N^2도 무시했으니 N을 무시하는 것도 가능하다.

이처럼 수식에서 지배적이지 않은 항은 무시해도 된다.

• O(N^2+N) ⇒ O(N^2)
• O(N+logN) ⇒ O(N)
• O(5*2^N + 1000N^100) ⇒ O(2^N)

하지만 여전히 수식에 합이 남아있을 수 있다.

O(B^2+A)는 하나의 항으로 줄일 수 없다. (A를 B로 표현가능하거나, B를 A로 표현 가능하지 않는 이상)

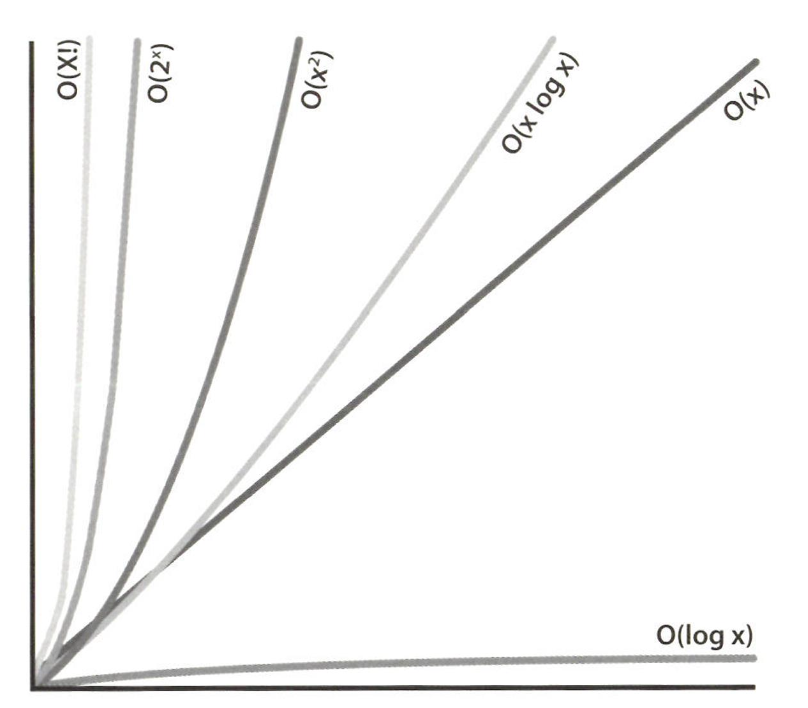
big-O 시간의 증가율

\[O(logN) < O(N) < O(NlogN) < O(N^2) < O(2^N) < O(N!)\]

[ 여러 부분으로 이루어진 알고리즘: 덧셈 vs 곱셈 ]

덧셈 수행 시간: O(A+B)

for (int a : arrA) {
		print(a);
}
for (int b: arrB) {
		print(b);
}

곱셈 수행 시간: O(A*B)

for (int a : arrA) {
		for (int b : arrB) {
				print(a + "," + b);
		}
}

왼쪽 예제에서 A일을 한 뒤 B의 일을 수행한다. 따라서 전체 수행한 일은 O(A+B)이다.

오른쪽 예제에서는 A의 각 원소에 대해 B의 일을 수행한다. 따라서 전체 수행한 일은 O(A*B)가 된다.

• A일과 B의 일이 별개로 이루어 진다 → 수행시간의 합
• A일을 할 때 B 일이 수행된다. 혹은 그 반대 → 수행시간의 곱

[ 상환 시간 ]

ArrayList(동적 가변크기 배열)의 삽입 연산의 수행시간

• 배열이 가득 차 있는 경우(드문 경우)

  배열에 N개의 원소가 들어 있을 때 새로운 원소를 삽입하려면 O(N)이 걸린다.

  → 크기가 2N인 배열을 새로 만들고 기존의 모든 원소를 새 배열로 복사해야 하기 때문

• 배열이 가득 차 있지 않은 경우(평상시 경우)

  삽입 연산은 O(1)이 걸린다.

두 가지 경우를 포함한 전체 수행 시간을 따져 볼 때, 상환 시간이라는 개념을 이용한다.

상환 시간: 최악의 경우는 가끔 발생하지만 한 번 발생하면 그 후로 꽤 오랫동안 나타나지 않으므로 비용(수행 시간)을 분할 상환한다는 개념

그렇다면 ArrayList의 경우 상환시간은?

배열의 크기가 2의 승수가 되었을 때 원소를 삽입하면 용량이 2배로 증가

배열의 크기가 1, 2, 4, 8, 16, … , X일 때 새로운 원소를 삽입하면 배열의 용량 2배로 증가 후 기존 원소를 새로운 배열로 복사해주어야 한다.

이때 합 1+2+4+8+16+…+X 은? 이 수열을 차례로 읽으면 1에서 X까지 두 배씩 증가하는 수열이다.

X+X/2+X/4+X/8+…+1의 합은 대략 2X와 같다.

→ 따라서 X개의 원소를 삽입했을 때 필요한 시간은 O(2X)이고, 이를 분할 상환해보면 삽입 한 번에 필요한 시간은 O(1)이다.

[ log N 수행 시간 ]

대표적인 예시로 이진탐색(binary search)가 있다.

이진탐색

• N개의 정렬된 원소가 들어 있는 배열에서 원소 x를 찾을 때 사용된다.
• 원소 x와 배열의 중간 값을 비교
  • x = 중간값 : 반환
  • x < 중간값 : 배열의 왼쪽 부분 재탐색
  • x > 중간값 : 배열의 오른쪽 부분 재탐색

  

각 동작이 수행될 때마다 탐색해야할 원소의 개수가 N/2로 줄어든다. 그러다가 원소를 찾았거나 탐색해야할 원소가 하나만 남으면 탐색을 중지한다.

총 수행 시간은 N을 절반씩 나누는 과정에서 몇 단계 만에 1이 되는지에 따라 결정된다.

반대로 생각해보면 1에서 16으로 증가할 때 2를 몇 번 곱해야 N이 되는지 확인해본다.

즉, 2^k = N을 만족하는 k는 logN이다.

어떤 문제에서 원소의 개수가 절반씩 줄어든다면 그 문제의 수행 시간은 O(logN)이 될 가능성이 크다.

같은 원리로, 균형 이진 탐색 트리(balanced binary search tree)에서 원소를 찾는 문제도 O(logN)이다.

→ 매 단계마다 원소의 대소를 비교한 후 왼쪽 혹은 오른쪽으로 내려간다. 각 단계에서 검색해야할 노드의 개수가 절반씩 줄어들게 된다.

[ 재귀적으로 수행 시간 구하기 ]

아래 코드는 수행 시간을 구하기 약간 까다롭다.

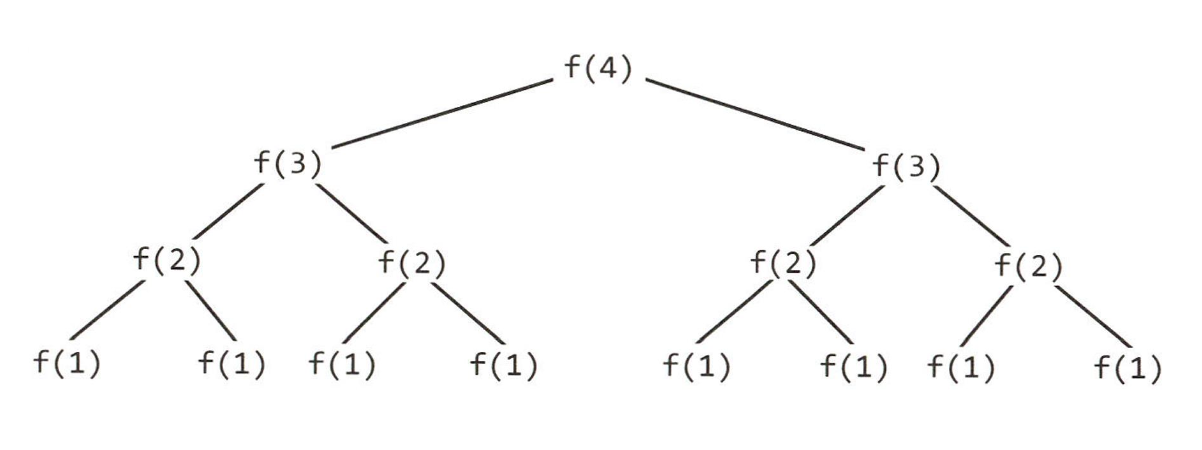
int f(int n) {
		if (n <= 1) {
				return 1;
		}
		return f(n - 1) + f(n - 1);
}

함수 f가 두 번 호출된 것을 보고 O(N^2)라 결론 내린다면 틀렸다.

트리의 깊이가 N이고, 각 노드(함수 호출)는 두 개의 자식 노드를 가지고 있다.

따라서 깊이가 한 단계 깊어질 때마다 이전의 두 배 더 많이 호출한다.

따라서 전체 노드의 개수는

\[2^0 + 2^1 + 2^2 + 2^3 + 2^4 + … + 2^N (=2^{N+1} - 1)\]

이처럼 보통 재귀 함수에서 수행시간은 O(분기^깊이)로 표현되곤 한다. 따라서 위의 경우 수행시간은 O(2^N)이 된다.

이 알고리즘의 공간 복잡도는 O(N)이 될 것이다. 전체 노드의 개수는 O(2^N)이지만, 특정 시각에 사용하는 공간의 크기는 O(N)이다.