🐹 4. Trees and Graphs

[ 트리의 종류 ]

트리는 노드로 이루어진 자료구조이다.

• 트리는 하나의 루트 노드를 갖는다
• 루트 노드는 0개 이상의 자식 노드를 갖고 있다.
• 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.

트리에는 사이클(cycle)이 존재할 수 없다. 노드들은 특정 순서로 나열될 수도 있고 그럴 수 없을 수도 있다. 각 노드는 어떤 자료형으로도 표현 가능하다.

Node 클래스를 간단하게 정의하면 다음과 같다.

class Node {
    public String name;
    public Node[] children;
}

노드 클래스를 포함하는 Tree 클래스를 정의할 수도 있지만, 굳이 하지 않겠다.

트리 vs 이진트리

이진트리(binary tree) : 각 노드가 최대 두 개의 자식을 갖는 트리

모든 트리가 이진트리는 아니다.

자식이 없는 노드는 ‘말단’ 노드라고 부른다.

이진 트리 vs 이진 탐색 트리

이진 탐색 트리 : 모든 노드가 ‘모든 왼쪽 자식들 ≤ n < 모든 오른쪽 자식들’ 속성을 가지는 이진트리

트리 문제가 주어졌을 때 보통 이진 탐색 트리일 것이라 가정해 버리는데, 이진 탐색 트리인지 아닌지 확실히 하도록 해야한다.

균형 vs 비균형

균형을 잡는다는 것이 왼쪽과 오른쪽 부분 트리의 크기가 완전히 같게 하는 것을 의미하지 않는다. ‘균형’ 트리인지 아닌지 확인하는 방법 중 하나는 ‘너무 불균형한건 아닌지’ 확인하는 것 이상의 의미를 갖는다. O(logN) 시간에 insert와 find를 할 수 있을 정도로 균형이 잘 잡혀 있지만, 그렇다고 꼭 완벽하게 균형 잡혀 있을 필요는 없다.

• 균형 트리의 일반적 유형
  • 레드-블랙 트리
  • AVL 트리

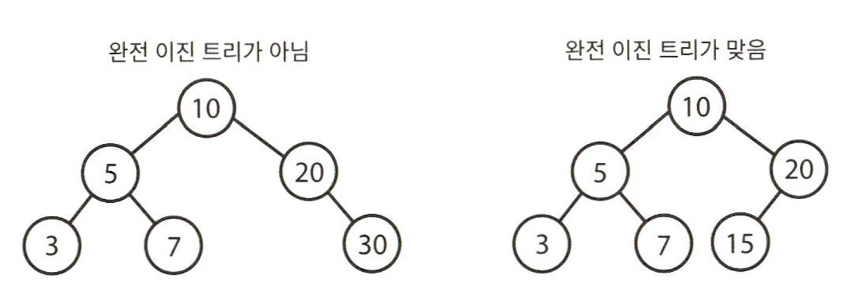
완전 이진 트리(complete binary tree)

: 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리

마지막 단계(level)는 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.

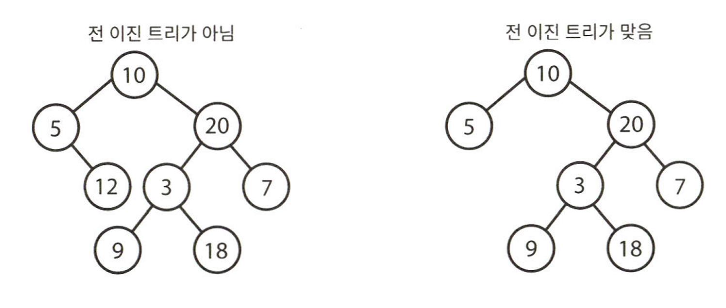
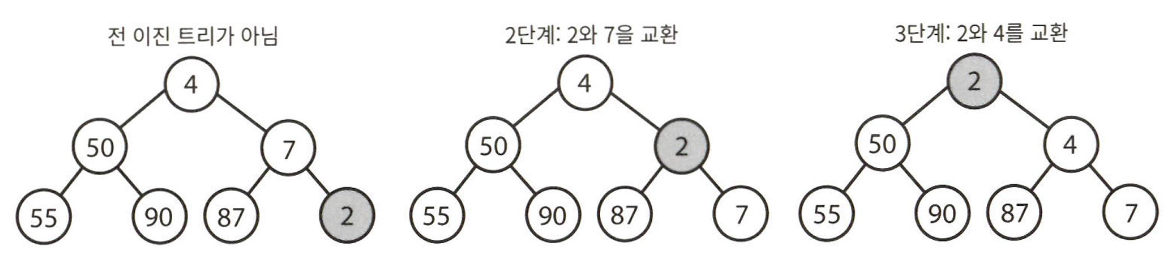
전 이진 트리(full binary tree)

: 모든 노드의 자식이 없거나 정확히 두 개 있는 경우

자식이 하나만 있는 노드가 존재해서는 안 된다.

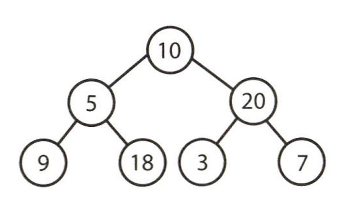
포화 이진 트리(perfect binary tree)

: 전 이진 트리이면서 완전 이진 트리인 경우

모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.

포화 이진 트리는 노드의 개수가 정확히 \(2^{k-1}\) (\(k\)는 트리의 높이)개여야 한다.

[ 이진 트리 순회 ]

중위(in-order), 후위(post-order), 전위(pre-order)

이 중 가장 빈번하게 사용되는 순회 방식은 중위 순회이다.

중위 순회(in-order traversal)

: 왼쪽 가지(branch), 현재 노드, 오른쪽 가지 순서로 노드를 ‘방문’하고 출력하는 방법

void inOrderTraversal(TreeNode node) {
    if (node != null) {
        inOrderTraversal(node.left);
        visit(node);
        inOrderTraversal(node.right);
    }
}

이진 탐색 트리를 이 방식으로 순회한다면 오름차순으로 방문하게 된다.

전위 순회(pre-order traversal)

: 자식 노드보다 현재 노드를 먼저 방문하는 방법

void preOrderTraversal(TreeNode node) {
    if (node != null) {
        visit(node);
        preOrderTraversal(node.left);
        preOrderTraversal(node.right);
    }
}

전위 순회에서 가장 먼저 방문하게 될 노드는 언제나 루트이다.

후위 순회(post-order traversal)

: 모든 자식 노드들을 먼저 방문한 뒤 마지막에 현재 노드를 방문하는 방법

void postOrderTraversal(TreeNode node) {
    if (node != null) {
        postOrderTraversal(node.left);
        postOrderTraversal(node.right);
        visit(node);
    }
}

후위 순회에서 가장 마지막에 방문하게 될 노드는 언제나 루트이다.

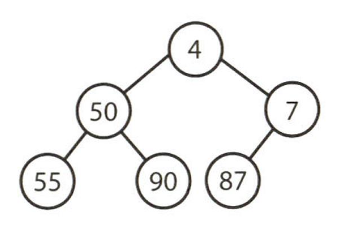
[ 이진 힙(최소힙과 최대힙) ]

최소힙(min-heaps)만 다룰 것이다. 최대힙(max-heaps)은 원소가 내림차순으로 정렬되어 있다는 점만 다를 뿐, 최소힙과 완전히 같다.

최소힙은 트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있다는 점에서 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다는 특성이 있다. 따라서 루트는 트리 전체에서 가장 작은 원소가 된다.

최소힙에는 insert와 extract_min이라는 핵심 연산 두 가지가 존재한다.

삽입

최소힙에 원소를 삽입할 때는 언제나 트리의 밑바닥에서부터 삽입을 시작한다. 완전 트리의 속성에 위배되지 않게 새로운 원소는 밑바닥 가장 오른쪽 위치로 삽입된다.

새로 삽입된 원소가 제대로 된 자리를 찾을 때까지 부모 노드와 교환해나간다. 기본적으로 이와 같은 방식으로 최소 원소를 위쪽으로 올린다.

힙에 있는 노드의 개수를 n이라 할 때 위의 연산은 O(log n) 시간이 걸린다.

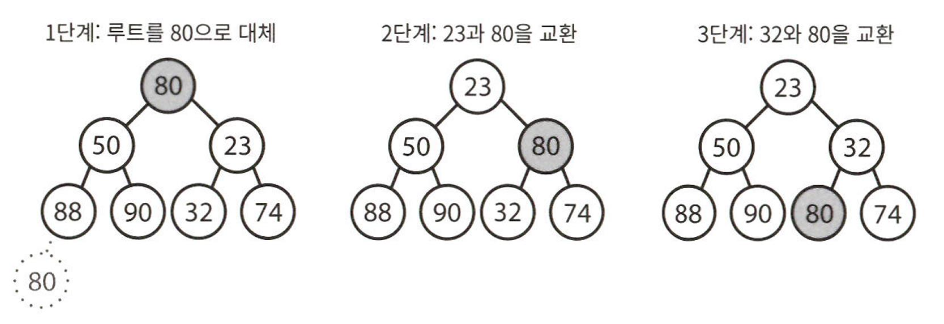
최소 원소 뽑아내기

최소힙에서 최소 원소는 언제가 가장 위에 놓인다.

1. 최소 원소를 제거한 후에 힙에 있는 가장 마지막 원소(밑바닥 가장 왼쪽)와 교환한다.
2. 최소힙의 성질을 만족하도록, 해당 노드를 자식 노드와 교환해 나감으로써 밑으로 내보낸다.(왼쪽 원소, 오른쪽 원소 중 더 작은 원소와 교환)

O(log n) 시간이 걸린다.

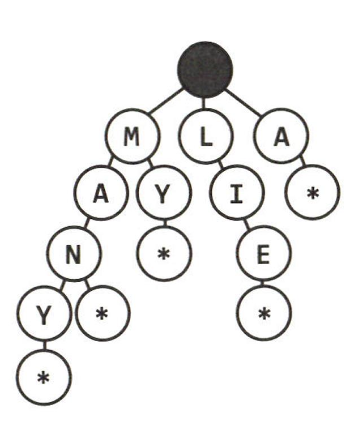
[ 트라이(접두사 트리) ]

: n차 트리(n-ary tree)의 변종으로 각 노드에 문자를 저장하는 자료구조

트리를 아래쪽으로 순회하면 단어 하나가 나온다.

널 노드(null node)라고도 불리우는 ‘* 노드’는 종종 단어의 끝을 나타낸다.

ex) MANY 이후 ‘* 노드’가 나오면 MANY라는 단어가 완성되었음을 알린다.

MA라는 경로가 존재한다는 사실은 MA로 시작하는 단어가 있다는 것이다.

트라이에서 각 노드는 1개에서 ALPHABET_SIZE + 1개까지 자식을 갖고 있을 수 있다. (만약 ‘* 노드’ 대신 boolean 플래그로 표현했다면 0개에서 ALPHABET_SIZE까지)

접두사를 빠르게 찾아보기 위한 아주 흔한 방식으로, 모든 언어를 트라이에 저장해놓는 방식이 있다.

해시테이블을 이용하면 주어진 문자열이 유효한지 아닌지 빠르게 확인할 수 있지만, 그 문자열이 어떤 유효한 단어의 접두사인지 확인할 수는 없다. 트라이를 이용하면 아주 빠르게 확인할 수 있다.

→ 트라이는 길이가 K인 문자열이 주어졌을 때 O(K) 시간에 해당 문자열이 유효한 접두사인지 확인할 수 있다. 이 시간은 해시테이블을 사용했을 때와 정확히 같은 수행 시간이다. 검색 O(1) 입력 문자열 읽기 O(K)

유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.

트리에서 연관된 접두사를 반복적으로 검색해야 하는 상황에서(ex. M, MA, MAN, MANY를 차례대로 살펴보는 상황), 트리의 현재 노드를 참조값으로 넘길 수도 있다. → 검색할 때마다 루트에서 시작할 필요가 없고, 단순히 Y가 MAN의 자식인지만 확인해보면 된다.

[ 그래프 ]

트리(tree)는 그래프(graph)의 한 종류이다. 트리는 사이크이 없는 하나의 연결 그래프이다.

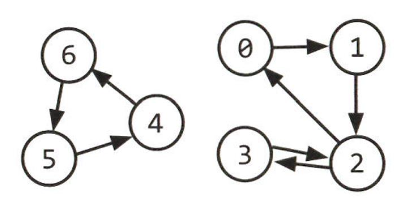
그래프: 단순히 노드와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 것

• 그래프에는 방향성이 있을 수도 있고 없을 수도 있다.
  • 방향성O : 일방통행
  • 방향성X : 양방향 통행
• 그래프는 여러 개의 고립된 부분 그래프로 구성될 수 있다.
• 그래프에는 사이클이 존재할 수도 있고 존재하지 않을 수도 있다.
  • 사이클 없는 그래프는 ‘비순환 그래프’(acycle graph)라고 부른다.

인접 리스트(adjacency list)

그래프를 표현할 때 사용되는 가장 일반적인 방법으로 모든 정점(혹은 노드)를 인접 리스트에 저장한다. 무방향 그래프에서 (a, b) 간선은 두 번 저장된다.

그래프에서 노드를 정의하는 간단한 클래스는 트리의 노드 클래스와 궁극적으로 같아 보인다.

class Graph {
    public Node[] nodes;
}
class Node {
    public String name;
    public Node[] children;
}

트리에선 특정 노드 하나에서 다른 노드로 모두 접근 가능하기 때문에 Tree 클래스를 따로 두지 않았다. 하지만 그래프는 트리와 달리 특정 노드에서 다른 모든 노드로 접근이 가능하지는 않아 Graph 라는 클래스를 사용한다.

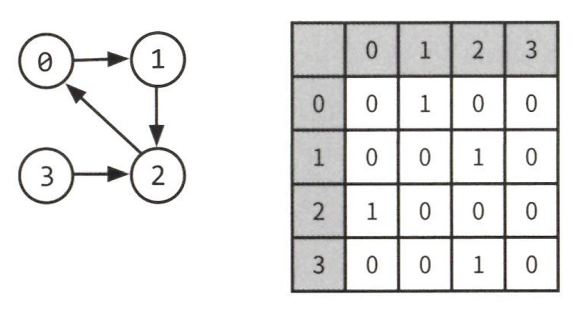
인접 행렬

$N\times N$ 불린 행렬(boolean matrix)로써 matrix[i][j]가 true라면 i에서 j로의 간선이 있다는 뜻이다. 여기서 N은 노드의 개수를 뜻한다.

그래프 탐색

일반적인 방법으로는 깊이 우선 탐색(depth-first search), 너비 우선 탐색(breadth-first search)이 있다.

• 깊이 우선 탐색(DFS)
  • 루트 노드에서 시작하여 해당 분기를 완벽하게 탐색하는 방법
  • 그래프에서 모든 노드를 방문하고자 할 때 더 선호됨
• 너비 우선 탐색(BFS)
  • 루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법
  • 최단 경로 혹은 임의의 경로를 찾고 싶을 때 선호됨

깊이 우선 탐색(DFS)

a 노드를 방문한 뒤 a와 인접한 노드들을 차례로 순회한다.

전위 순회를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.

이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다는 것이다. 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.

void search(Node root) {
    if (root == null) return;
    visit(root);
    root.visited = true;
    for each (Node n in root.adjacent) {
        if (n.visited == false) {
                search(n);
        }
    }
}

너비 우선 탐색(BFS)

BFS는 재귀적으로 동작하지 않는다. 큐(queue)를 사용한다.

a 노드에서 시작한다고 했을 때, BFS는 a 노드의 이웃 노드를 모두 방문한 다음에 이웃의 이웃들을 방문한다. 즉, 거리에 따라 단계별로 탐색한다.

void search(Node root) {
    Queue queue = new Queue();
    root.marked = true;
    queue.enqueue(root); // 큐의 끝에 추가한다.

    while (!queue.isEmpty()) {
        Node r = queue.dequeue(); // 큐의 앞에서 뽑아낸다.
        visit(r);
        foreach (Node n in r.adjacent) {
            if (n.marked == false) {
                n.marked = true;
                queue.enqueue(n);
            }
        }
    }
}

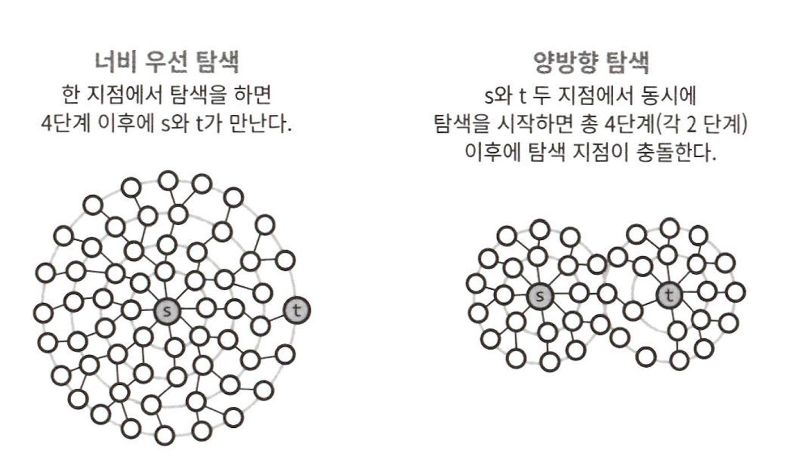
양방향 탐색

양방향 탐색(bidirectional search)은 출발지와 도착지 사이에 최단 경로를 찾을 때 사용되곤 한다. 기본적으로 출발지와 도착지 두 노드에서 동시에 너비 우선 탐색을 수행한 뒤, 두 탐색 지점이 충돌하는 경우에 경로를 찾는 방식이다.

양방향 탐색 방식이 왜 더 빠른지 살펴본다. 모든 노드가 적어도 k개의 이웃 노드와 연결되어 있고 s에서 t로의 최단 거리가 d가 되는 그래프를 생각해 보자.

• 전통적인 BFS를 사용한다면 첫 단계에서 k개의 노드를 탐색해야 한다. 다음 단계에선 k개의 노드들 또한 이웃한 k개의 노드를 탐색해야 하므로 총 $k^2$개의 노드를 탐색해야 한다.

  → 따라서 이를 d번 반복하면 총 $O(k^d)$개의 노드를 탐색해야 한다.

• 양방향 탐색을 사용한다면 두 탐색 알고리즘이 대략 d/2 단계(s와 t 사이의 중간지점)까지 탐색한 후에 충돌할 것이다. 따라서 s와 t 각각에서 방문하게 될 노드의 수는 대략 $k^{d/2}$개가 될 것이고,

  → 따라서 방문하게 될 전체 노드는 대략 $2k^{d/2}$, $O(k^{d/2})$개가 된다.