🐹 5. Sorting

10. 정렬과 탐색

1. 선택 정렬(selection sort)

→ 평균 및 최악 실행 시간: $O(n^2)$, 메모리: $O(1)$

선택정렬은 심플하지만 비효율적이다.

[ 정렬 방법 ]

1. 배열을 선형 탐색하며 가장 작은 원소를 배열 맨 앞으로 보낸다.(맨 앞에 있던 원소와 자리를 바꾼다.)
2. 그 다음으로 두 번째로 작은 원소를 찾은 뒤 앞으로 보내준다.
3. 모든 원소가 정렬될 때까지 반복한다.

[ 최선과 최악의 경우 ]

• 최선의 경우 : 이미 정렬되어 있는 경우를 생각해볼 수 있다
• 최악의 경우 : 역순으로 정렬되어 있는 경우를 생각해볼 수 있다.

선택 정렬은 최선의 경우와 최악의 경우 모두 탐색의 횟수는 $N^2$ 이므로 결과적으로 모두 $O(N^2)$의 시간복잡도를 갖는다.

[ 코드 ]

void selectionSort(int[] arr) {
    for (int i = 0; i < N - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < N; j++) {
            if (arr[minIndex] > arr[j]) {
                minIndex = j;
            }
        }
        int temp = arr[minIndex];
        arr[minIndex] = arr[i];
        arr[i] = temp;
    }
}

2. 삽입 정렬(insertion sort)

→ 평균 및 최악의 실행 시간: $O(N^2)$, 메모리: $O(1)$

보통의 경우 삽입 정렬보다 퀵 정렬이 효율적이나 정렬이 거의 되어 있는 상황에서는 퀵 정렬 알고리즘보다 더 강력하다.

[ 정렬 방법 ]

1. 배열을 선형 탐색하며 현재 index가 index 앞까지의 부분에서 삽입될 위치를 찾아 삽입한다.
2. index를 1씩 키운다.
3. 모든 원소가 정렬될 때까지 반복한다.

[ 최선과 최악의 경우 ]

• 최선의 경우 : 이미 정렬이 되어있는 경우 → $O(N)$

  한 번씩밖에 비교를 하지 않기 때문에 $O(N)$

• 최악의 경우 : 역순으로 정렬된 경우 → $O(N^2)$

[ 코드 ]

void insertionSort(int[] arr) {
    for (int i = 1; i < N; i++) {
        int temp = arr[i];
        int prev = i - 1;
        for (j = i - 1; j >= 0; j++) {
            if (arr[j] > temp) {
                arr[j+1] = arr[j];
                prev = j;
            } else {
                break;
            }
        arr[prev] = temp;
    }
}

3. 힙 정렬(heap sort)

→ 평균 및 최악의 실행 시간: $O(NlogN)$, 메모리: $O(1)$

시간복잡도가 $O(NlogN)$이긴 하지만 실제로는 동일한 시간 복잡도를 가진 다른 정렬 알고리즘(ex. Quick sort)보다 느리다.

[ 자료구조 힙(Heap)이란? ]

: 완전 이진 트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조

여러 개의 값들 중에서 최댓값과 최솟값을 빠르게 찾아내도록 만들어진 자료구조

• 힙은 반정렬 상태(느슨한 상태)를 유지한다
  • 큰 값이 상위 레벨에 있고, 작은 값이 하위 레벨에 있음
  • 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리
• 중복된 값을 허용한다.

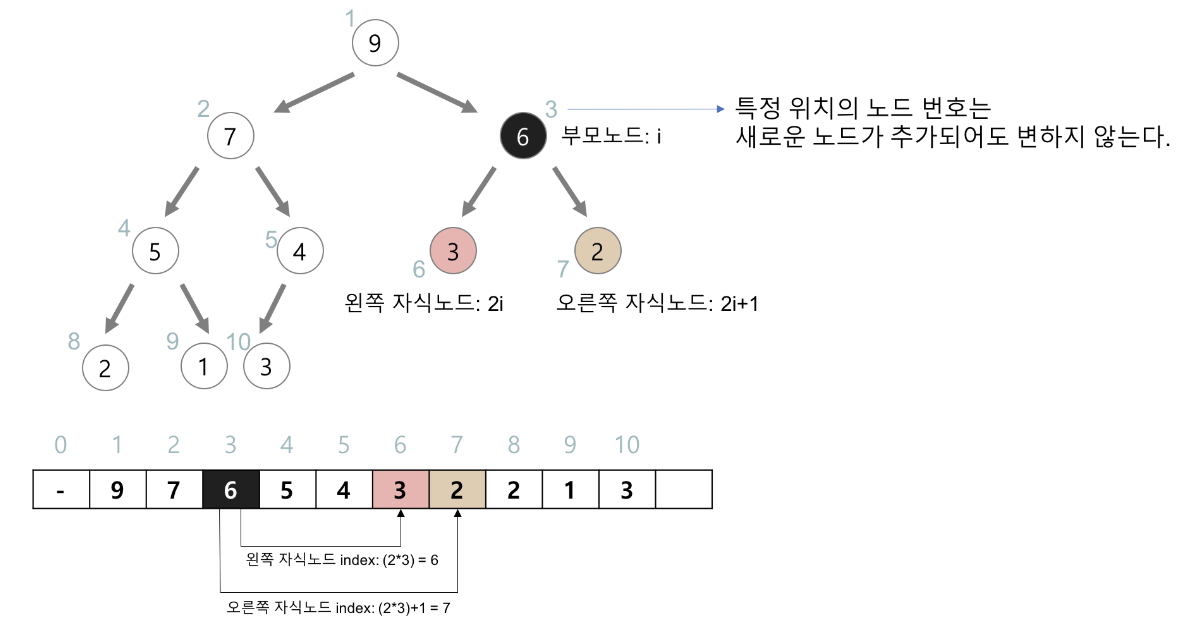
[ 힙(heap) 구현 ]

• 힙을 저장하는 표준적인 자료구조 → 배열
• 구현을 쉽게 하기 위해 첫 번째 인덱스인 0은 사용되지 않는다.

• 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.

  ex) 루트 노드의 오른쪽 노드의 번호는 항상 3이다.

• 힙에서의 부모 노드와 자식 노드의 관계
  • 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
  • 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
  • 부모의 인덱스 = (자식의 인덱스) / 2

  

public class Heap<E> {

    private final Comparator<? super E> comparator;
    private static final int DEFAULT_CAPACITY = 10;

    private int size;  // 요소 개수

    private Object[] array;  // 요소를 담을 배열

    // 생성자 Type 1 (초기 공간 할당 X)
    public Heap() {
        this(null);
    }

    public Heap(Comparator<? super E> comparator) {
        this.array = new Object[DEFAULT_CAPACITY];
        this.size = 0;
        this.comparator = comparator;
    }

    // 받은 인덱스의 부모 노드 인덱스를 반환
    private int getParent(int index) {
        return index / 2;
    }

    // 받은 인덱스의 왼쪽 자식 노드 인덱스를 반환
    private int getLeftChild(int index) {
        return index * 2;
    }

    // 받은 인덱스의 오른쪽 자식 노드 인덱스를 반환
    private int getRightChild(int index) {
        return index * 2 + 1;
    }
}

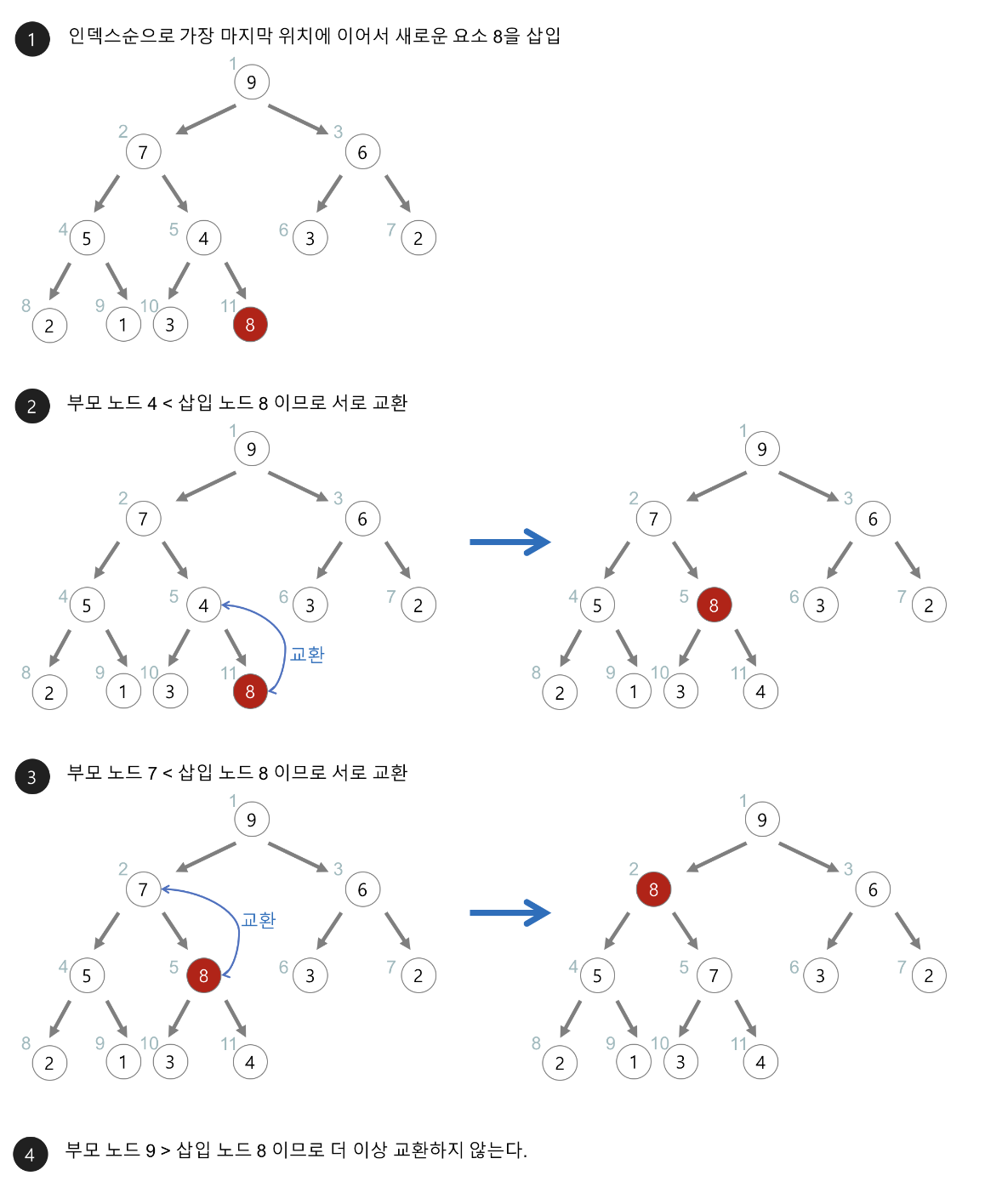
[ 힙(heap)의 삽입 ]

1. 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
2. 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.

/* 최대힙 삽입 */
void insertMaxHeap(int x) {
    maxHeap[++heapSize] = x; // 힙 크기 하나를 증가하고 마지막 노드에 x를 넣는다
    
    for (int i = heapSize; i > 1; i/=2) {
        // 마지막 노드가 자신의 부모 노드보다 크면 swap
        if (maxHeap[i/2] < maxHeap[i]) {
            swap(i/2, i);
        } else {
            break;
        }
    }
}

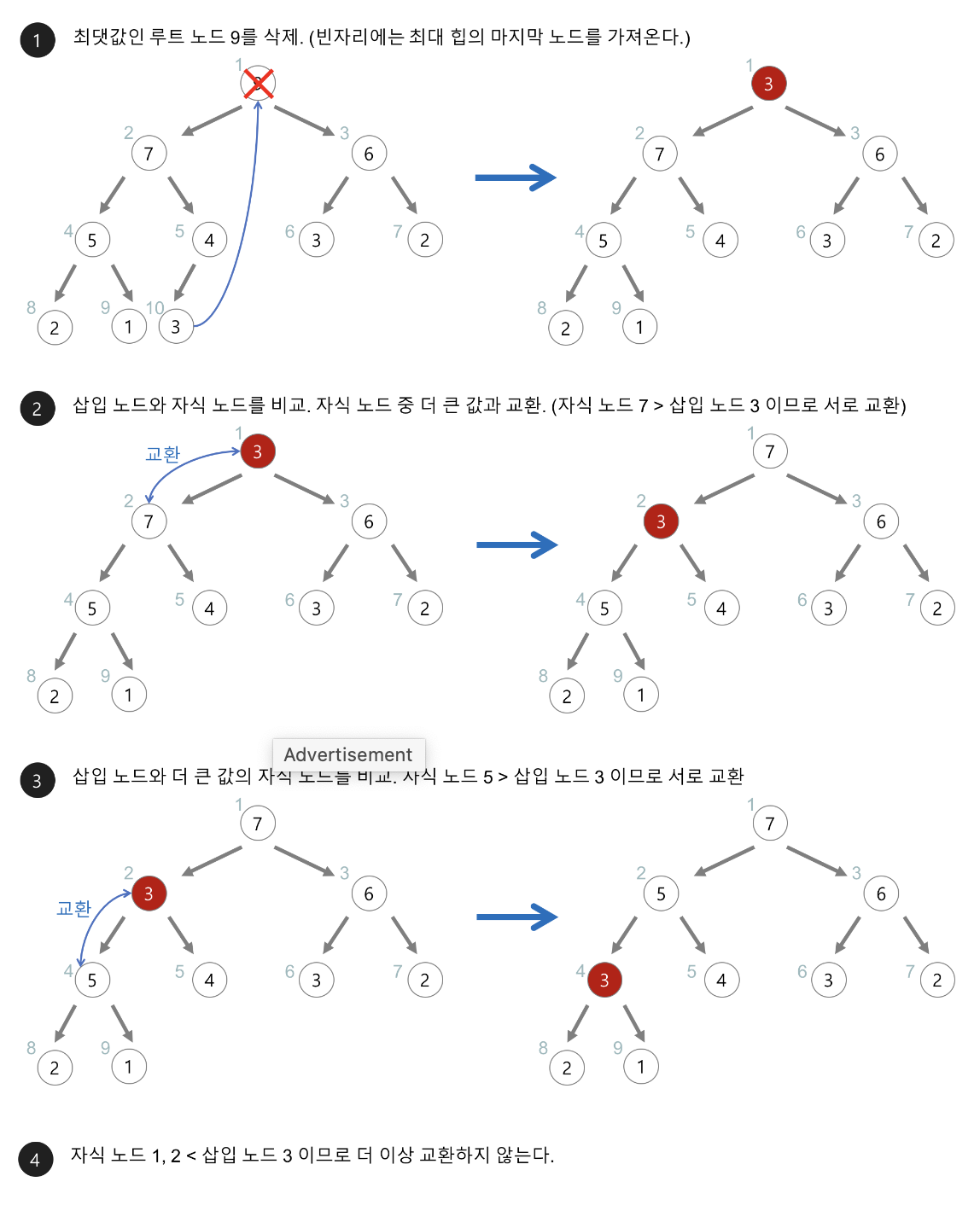
[ 힙(heap)의 삭제 ]

1. 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.

   최대 힙에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.

2. 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
3. 힙을 재구성한다.

/* 최대힙 삭제 */
int deleteMaxHeap() {
    if (heapSize == 0) { //배열이 빈 경우
            return 0;
    }
    
    int item = maxHeap[1]; // 루트 노드의 값을 저장한다. 
    maxHeap[1] = maxHeap[heapSize]; // 마지막 노드의 값을 루트 노드에 넣는다.
    maxHeap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드를 0으로 초기화한다. 

    for (int i = 1; i*2 <= heapSize; ) {
        // 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 반복문을 나간다.
        if (maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2]) {
            break;
        }
        // 왼쪽 노드가 더 큰 경우, 왼쪽 노드와 마지막 노드를 swap
        else if (maxHeap[i*2] > maxHeap[i*2+1] {
            swap(i, i*2);
            i = i*2;
        }
        // 오른쪽 노드가 더 큰 경우, 오른쪽 노드와 마지막 노드를 swap
        else {
            swap(i, i*2+1);
            i = i*2+1;
        }
    }
    return item;
}

[ 최선과 최악의 경우 ]

힙 정렬은 최선, 평균, 최악 모두 O(NlogN)의 시간복잡도를 가진다.

4. 퀵 정렬(quick sort)

→ 평균 실행 시간: $O(NlogN)$, 최악 실행 시간: $O(N^2)$, 메모리: $O(logN)$

최악의 경우 실행시간이 힙 정렬보다 느리지만 일반적으로 퀵 정렬을 사용한다.

힙 정렬과 퀵 정렬 모두 swap이 사용되는데 데이터의 양이 많을 때 힙 정렬이 훨씬 더 많은 swap이 실행되면서 최악의 경우가 아니라면 퀵 정렬이 더 빠르다.

[ 정렬 방법 ]

1. 무작위로 선정된 한 원소를 사용하여 배열을 분할한다.

2. 선정된 원소보다 작은 원소들은 앞에, 큰 원소들은 뒤로 보낸다.

   배열 분할 작업은 연속된 swap 연산을 통해 효율적으로 수행된다

배열과 그 부분 배열을 반복적으로 분할해 나가면 결국에 배열은 정렬된 상태에 도달한다.

하지만 배열 분할에 사용되는 원소가 중간값, 적어도 중간값에 가까운 값이 되리라는 보장이 없기 때문에, 정렬 알고리즘이 느리게 동작할 수도 있다.

[ 최선과 최악의 경우 ]

• 최악의 경우 : pivot 값이 최소나 최대값으로 지정되어 파티션이 나누어지지 않았을 때 → $O(N^2)$

[ 코드 ]

void quickSort(int[] arr, int left, int right) {
    int index = partition(arr, left, right);
    if (left < index - 1) { // 왼쪽 절반 정렬
        quickSort(arr, left, index - 1);
    }
    if (index < right) { // 오른쪽 절반 정렬 
        quickSort(arr, index, right);
    }
}

int partition(int[] arr, int left, int right) {
    int pivot = arr[(left + right) / 2]; // 분할 기준 원소 선정
    while (left <= right) {
        // 왼쪽에서 오른쪽으로 옮겨야 하는 원소 탐색
        while (arr[left] < pivot) left++;

        // 오른쪽에서 왼쪽으로 옮겨야 하는 원소 탐색
        while (arr[right] > pivot) right--;

        // 원소를 스왑한 뒤 left와 right를 이동
        if (left <= right) {
            swap(arr, left, right); // 스왑
            left++;
            right--;
        }
    }
    return left;
}

5. 병합 정렬(merge sort)

→ 평균 및 최악 실행 시간: $O(NlogN)$, 메모리: 상황에 따라 다름

배열을 분할했다가 ‘병합’을 처리하는 과정이 가장 복잡하다.

[ 병합 작업 ]

1. 병합 대상이 되는 배열의 두 부분을 임시 배열(helper)에 복사한다.
2. 왼쪽 절반의 시작 지점(helperLeft)와 오른쪽 절반의 시작 지점(helperRight)를 추적한다.
3. helper를 순회하면서 두 배열에서 더 작은 값의 원소를 꺼내어 원래 배열에 복사해 넣는다.
4. 두 배열 중 한 배열에 대한 순회가 끝난 경우에는 다른 배열의 남은 부분을 원래 배열에 남김없이 복사해 넣고 작업을 마친다.

[ 코드 ]

void mergesort(int[] array) {
    int[] helper = new int[array.length];
    mergesort(array, helper, 0, arraay.length - 1);
}

void mergesort(int[] array, int[] helper, int low, int high) {
    if (low < high) {
        int middle = (low + high) / 2;
        mergesort(array, helper, low, middle); // 왼쪽 절반 정렬
        mergesort(array, helper, middle+1, high); // 오른쪽 절반 정렬
        merge(array, helper, low, middle, high); // 병합
    }
}

void merge(int[] array, int[] helper, int low, int middle, int high) {
    /* 절반짜리 두 배열을 helper 배열에 복사한다. */
    for (int i = low; i <= high; i++) {
        helper[i] = array[i].
    }

    int helperLeft = low;
    int helperRight = middle + 1; 
    int current = low;

    /* helper 배열 순회. 왼쪽 절반과 오른쪽 절반을 비교하여 작은 원소를
        * 원래 배열에 복사해 넣는다. */
    while (helperLeft <= middle && helperRight <= high) {
        if (helper[helperLeft] <= helper[helperRight]) {
                array[current] = helper[helperLeft];
                helperLeft++;
        } else { // 오른쪽 원소가 왼쪽 원소보다 작으면
                array[current] = helper[helperRight];
                helperRight++;
        }
        current++;
    }

    /* 왼쪽 절반 배열에 남은 원소들을 원래 배열에 복사해 넣는다. */
    int remaining = middle - helperLeft;
    for (int i = 0; i <= remaining; i++) {
        array[current + i] = helper[helperLeft + i];
    }
}