🐹 9. Math & Logic puzzles

06. 수학 및 논리 퍼즐

[ 소수 ]

모든 자연수는 소수의 곱으로 나타낼 수 있다는 규칙이 있다.

\[84=2^2* 3^1*5^0*7^1*11^0*13^0*17^0* \cdots\]

위의 수식에서 많은 소수의 지수 부분이 0이다.

가분성(divisibility)

위에 언급한 규칙에 따르면 어떤 수 x로 y를 나눌 수 있으려면 x를 소수의 곱으로 분할하였을 때 나열되는 모든 소수는 y를 소수의 곱으로 분할하였을 때 나열되는 모든 소수의 부분집합이어야 한다.

$x=2^{j0}3^{j1}5^{j2}7^{j3}11^{j4}* \cdots$ 이고

$y=2^{k0}3^{k1}5^{k2}7^{k3}11^{k4}* \cdots$ 일 때

x가 y로 나누어 떨어지면 $i, j_i \ge k_i$를 만족한다.

즉, x/y를 만족하려면 모든 i에 대해서 $j_i \ge k_i$를 만족해야 한다. 따라서 최대공약수는 다음과 같이 표현할 수 있다.

\[gcd(x, y) = 2^{min(j0, k0)}*3^{min(j1, k1)}*5^{min(j2, k2)}* \cdots\]

x와 y의 최소공배수는 다음과 같이 표현할 수 있다.

\[lcm(x, y) = 2^{max(j0, k0)}*3^{max(j1, k1)}*5^{max(j2, k2)}* \cdots\]

gcd*lcm을 하면 다음과 같은 결과가 나온다.

$gcdlcm = 2^{min(j0, k0)}2^{max(j0, k0)}3^{min(j1, k1)}3^{max(j1, k1)}*\cdots$

$=2^{min(j0,k0)+max(j0,k0)} * 3^{min(j1,k1)+max(j1,k1)}*\cdots$

$=2^{j0+k0}3^{j1+k1}\cdots$

$=2^{j0}2^{k0}3^{j1}3^{k1}\cdots$

$=xy$

소수판별

• 가장 단순한 방법 : 2에서 n-1까지 루프를 돌며 나누어지는 경우 확인

boolean primeNaive(int n) {
    if (n < 2) {
        return false;
    }
    for (int i = 2; i < n; i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

위 코드를 살짝 개선해 보면 루프를 n이 아닌 n의 제곱근까지만 돌면 된다.

boolean primeNaive(int n) {
    if (n < 2) {
        return false;
    }
    int sqrt = (int) Math.sqrt(n);
    for (int i = 2; i < sqrt; i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

$\sqrt{n}$까지만 검사해보면 충분하다. 왜냐하면 n을 나누는 모든 숫자 a는 그에 대한 보수 b(a*b=n)이가 반드시 존재하기 때문이다. 만일 $a > \sqrt{n}$이라면 $b< \sqrt{n}$이다($\sqrt{n}^2 =n$이므로). 따라서 n이 소수인지 알아보기 위해 a까지 검사할 필요가 없다. b에서 이미 검사했기 때문이다.

소수 목록 만들기: 에라토스테네스의 체

에라토스테네스의 체는 소수 목록을 만드는 굉장히 효율적인 방법이다. 이 알고리즘은 소수가 아닌 수들을 반드시 다른 소수로 나누어진다는 사실에 기반하여 동작한다.

처음 주어진 리스트는 1부터 max까지의 모든 수로 구성되어 있다.

1. 2로 나누어지는 모든 수를 리스트에서 없앤다.
2. 그 후 다음 소수, 즉 아직 지워지지 않은 수 중 가장 작은 수를 찾는다.
3. 그 수로 나누어지는 모든 수를 리스트에서 제거한다.

이런식으로 2, 3, 5, 7, 11 등의 소수로 나뉘는 모든 수들을 리스트에서 삭제한다. 그러고 나면 2에서 max까지의 구간 내에 있는 모든 소수들의 리스트가 만들어진다.

boolean[] sieveOfEratosthenes(int max) {
    boolean[] flags = new boolean[max+1];
    int count = 0;

    init(flags); //0과 1번 인덱스를 제외한 모든 원소값을 true로 초기화
    int prime = 2;

    while (prime <= Math.sqrt(max)) {
        /* prime의 배수들을 지워나간다. */
        crossOff(flags, prime);

        /* 그다음 true로 세팅된 인덱스를 찾는다. */
        prime = getNextPrime(flags, prime);
    }
    return flags;
}

void crossOff(boolean[] flags, int prime) {
    /* prime의 배수들을 제거해나간다. k < prime인 k에 대한 k * prime은
        * 이전 루프에서 이미 제거되었을 것이므로 prime * prime부터 시작한다. */
    for (int i = prime * prime; i < flags.length; i += prime) {
        flags[i] = false;
    }
}

int getNextPrime(boolean[] flags, int prime) {
    int next = prime + 1;
    while (next < flags.length && !flags[next]) {
        next++;
    }
    return next;
}

몇 가지 개선의 여지가 남아 있다. 간단하게는 배열에 홀수만 저장하는 방법이 있는데, 이 방법을 이용하면 메모리 공간을 반으로 줄일 수 있다.

[ 확률 ]

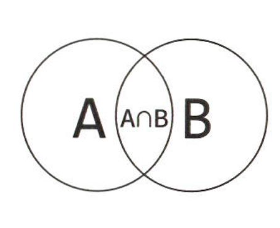
두 사건 A와 B를 나타내는 다음의 벤 다이어그램을 보자. 두 원이 점유하고 있는 영역은 각각의 상대적 확률을 나타내는 것이고, 겹치는 부분은 {A and B}의 사건을 나타낸다.

$A\cap B$의 확률

A에 떨어질 확률과 A와 B가 겹치는 부분의 비율도 알고 있다면(A에 속해 있으면서 B에도 속해있을 확률), 그 확률은 다음과 같이 표현할 수 있다.

\[P(A \cap B)=P(B|A)P(A)\]

예를들어, 1부터 10까지의 수 중 하나를 뽑는다 하자. 5보다 작거나 같으면서 동시에 짝수인 수를 뽑을 확률은 몇 인가? 1~5까지의 수를 뽑을 확률은 50%이고, 1~5중에서 짝수를 뽑을 확률은 40%다. 따라서 두 경우에 모두 속할 확률은 다음과 같다.

$P(x=짝수\cap x<=5)$

$=P(x=짝수 \cap x<=5)P(x<=5)$

$=(2/5)*(1/2)$

$=1/5$

$P(A \cap B)=P(B

A)P(A)=P(A

B)P(B)$ 이므로 B에 속하면서 A에도 속할 확률은 다음과 같이 반대로 표현할 수도 있다.

\[P(A|B)=P(B|A)P(A)/P(B)\]

위 수식을 베이즈 정리(Bayes’ Theorem)라고 부른다.

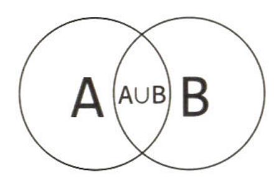
$A \cup B$의 확률

다트가 A 혹은 B에 떨어질 확률을 생각하자. 각 영역에 떨어질 확률은 알고 있고, 겹치는 부분에 떨어질 확률도 알고 있다면, A 혹은 B에 떨어질 확률은 다음과 같이 표현할 수 있다.

\[P(A\cup B)=P(A)+P(B)-P(A\cap B)\]

예를 들어, 우리가 1~10까지의 수 가운데 하나를 고른다고 생각해보자. 짝수를 고를 확률과 1~5까지의 수 중에서 하나를 뽑을 확률은? 짝수를 뽑을 확률은 50%이고, 1~5까지의 수를 뽑을 확률 또한 50%이다. 두 경우에 모두 속할 확률은 20%이다. 따라서 두 경우 중 하나에 속할 확률은 다음과 같다.

$P(x=짝수 \cup x <=5)$

$=P(x=짝수)+P(x<=5)-P(x=짝수\cap x<=5)$

$=1/2+1/2-1/5$

$=4/5$

여기서 독립사건과 상호 배타적인 사건의 확률을 구하는 특수 규칙들을 쉽게 얻을 수 있다.

독립성

A와 B가 독립사건(한 사건의 발생과 다른 사건의 발생 사이에 아무런 관계가 없는 경우)이라면, A가 B에 아무런 영향을 끼치지 않으므로, $P(B

A)=P(B)$가 되고 따라서 $P(A \cap B)=P(A)P(B)$가 된다.

상호 배타성(mutual exclusivity)

A와 B가 상호 배타적(한 사건이 일어난 경우 다른 사건은 발생할 수 없는 경우)이라면, $P(A \cap B)=0$이 되므로 $P(A \cup B)$를 계산할 때 $P(A \cap B)$ 항은 제거해도 된다. 따라서 $P(A \cup B)=P(A)+P(B)$가 된다.

독립과 상호 배타의 개념을 많이 혼동한다. 두 사건의 확률이 전부 0보다 큰 경우에 이 두 사건이 독립적이면서 상호 배타적인 것은 불가능하다.

→ 상호 배타성은 한 사건이 발생하면 다른 사건이 발생할 수 없다는 관계가 존재하지만 독립성은 한 사건의 발생 여부가 다른 사건에 아무런 영향도 미치지 않아야 하기 때문이다.

그러므로 두 사건의 확률이 전부 0보다 클 경우엔, 상호 배타성과 독립성을 동시에 만족시킬 수는 없다.

두 사건 중 하나의 확률이 0이라면(그런 사건이 일어나는 것이 불가능하다면), 두 사건은 독립적이면서 상호 배타적이다. 공식을 적용해보면 증명 가능하다.

[ 입을 열라 ]

수수께끼 같은 문제를 만나면 당황하지 말자. 알고리즘 문제와 마찬가지로, 면접관들이 원하는 것은 문제를 어떻게 공략해 나가는 지 보는 것이다. 문제를 어떻게 공략해 나가는지 면접관들에게 보여주자

[ 규칙과 패턴을 찾으라 ]

많은 경우에, 문제를 풀다가 발견하는 ‘규칙’이나 패턴은 반드시 적어두는 것이 좋다.

Q. 끈이 두 개 있다. 각 끈을 태우는 데 정확히 한 시간이 걸린다. 이 두 끈을 사용해 15분을 재려면 어떻게 해야 되겠는가? 이 끈의 밀도는 균일하지 않아서, 절반의 길이를 태우는 데 드는 시간이 정확히 30분이라는 보장이 없다.

우선 한 시간을 재는 방법, 두 시간을 재는 방법은 바로 알 수 있다. 끈 하나를 다 태운 뒤 다음 끈을 태우면 된다. 이 사실을 일반적인 규칙으로 만들어 보자.

이 끈을 가운데, 혹은 끝이 아닌 어딘가에서부터 태우는 것은 그다지 도움이 되지 않는다. 왜냐하면 불을 붙인 부분부터 양쪽으로 타들어갈텐데, 끈이 다 타는 데 시간이 얼마나 걸릴지 알 수 없기 때문이다.

하지만 동시에 양쪽 끝에 불을 붙일 수는 있다. 그러면 정확히 삼십 분 뒤에 끈은 다 타버린다.

이제 끈 하나로 30분을 잴 수 있다는 것은 알았다. 따라서 첫 번째 끈은 양쪽 끝에 불을 붙이고 두 번째 끈은 한 쪽 끝에 불을 붙인다면 두 번째 끈에서 30분을 태운 결과를 알 수 있다.

이제 규칙들을 조합해 보자. 전부 태우는 데 한 시간 걸리는 2번 끈을 30분 걸리는 끈으로 바꿀 수 있다. 그다음 2번 끈의 양쪽에 불을 붙여 버리면(규칙 2) 2번 끈은 15분 뒤에 전부 타버린다. 다음 순서대로 진행한다.

1. 1번 끈은 양쪽에 불을 붙이고, 2번 끈은 한쪽에만 불을 붙인다.
2. 1번 끈이 다 타들어가면 30분이 지난 것이다. 따라서 2번 끈이 다 타기 위해 남은 시간은 30분이다.
3. 그 시점에, 2번 끈의 다른 쪽에도 불을 붙인다.
4. 그러면 정확히 15분 뒤에, 2번 끈도 완전히 다 타버릴 것이다.

발견한 ‘규칙’을 나열하는 과정을 통해, 문제풀이 과정이 훨씬 쉬워졌다.

[ 최악의 경우는? ]

수수께끼 종류의 문제 중 많은 수가 최악의 경우를 최소화하는 것과 연관이 있다. 어떤 행동을 최소화하는 문제일 수도 있고, 지정됫 횟수 안에 처리해야 하는 문제일 수도 있다.

그럴 때는 최악의 상황을 ‘균형 맞추도록’하면 도움이 된다. 다시 말해, 초기의 어떤 결정을 통해 최악의 경우가 한 쪽 방향으로 쏠리면, 그 결정을 다른 방식으로 나눠 최악의 경우가 균형 잡히도록 할 수 있다.

Q. 공이 아홉 개 있다. 이 가운데 여덟 개는 무게가 같고, 하나는 좀 더 무겁다. 저울이 하나 주어지는데, 이 저울로는 왼쪽에 둔 공들이 무거운지, 아니면 오른쪽에 둔 공들이 무거운지 밖에 알아낼 수가 없다. 이 저울을 딱 두 번만 사용해서 가장 무거운 공을 찾아 내라.

먼저 떠올릴 수 있는 접근법은, 아홉 번째 공은 제쳐 둔 채, 나머지 공을 네 개씩 두 그룹으로 나누는 것이다. 만약 이 두 그룹의 무게가 같다면, 제쳐 뒀던 공이 가장 무거운 공이다. 그게 아니라면 더 무거운 그룹을 택해 반복한다. 그런데 이렇게 하면 최악의 경우 저울을 세 번 사용해야 하므로 낭패다.

이것이 ‘최악의 경우’가 균형 잡히지 않은 사례다. 제쳐 둔 공이 무거운 놈인지 알아내는 데에는 한 번이면 족하지만 남은 공들에서 무거운 공을 찾아내는 데에는 세 번이 걸린다. 만일 우리가 처음에 제쳐 놓는 공의 개수를 늘려 잡아 일종의 페널티를 주게 되면, 다른 그룹에 주어지는 부담을 좀 줄일 수 있다. 이것이 바로 ‘최악의 경우 균형을 가져다 주는’ 방법의 사례다.

1. 공들을 세 개씩 세 그룹으로 나눠 보면, 저울을 한 번만 사용해서 어떤 그룹에 무거운 공이 있는지 알아낼 수 있다. N개의 공이 주어지고 N이 3으로 나눌 수 있는 값이면, 저울을 한 번 써서 무거운 공이 속한 그룹(N/3 크기)을 알아낼 수 있다.
2. 남은 세 개의 공을 같은 방법으로 달아 보면 된다. 공 하나는 제쳐 놓고, 남은 두 개의 공을 저울 양쪽에 하나씩 올려 놓는다. 저울이 기운다면, 기운 쪽의 공이 무거운 놈이다. 아니라면, 제쳐 놓은 공이 무거운 놈이다.